Custom factor (unaryFactor) issue with initial heading

[nmahabadi]

Description

It seems that when using a custom factor for GPS measurements (UnaryFactor class as in the instructions) with a prior node with initial heading, the solvers in C++ cannot optimize and converge to the solutions. Setting the heading to 0° however poses no issue and the solvers can converge after some iterations even with noisy initial estimates. This has been tested both with synthetic data and real data and both give similar results but with the real data it is even worst.

Steps to reproduce

-------------------------------------------------------------------
If we extend LocalizationExample.cpp by adding a prior factor (PriorFactor) with a 90° heading as below and also updating the GPS data and initial estimates, then neither of the solvers (LevenbergMarquardtOptimizer / GaussNewtonOptimizer) can solve/converge. LevenbergMarquardtOptimizer throws the following for instance:

Levenberg-Marquardt giving up because cannot decrease error with maximum lambda

 // Add prior node with 90 deg heading
 auto priorNoise = noiseModel::Diagonal::Sigmas(Vector3(0.01, 0.01, 0.1)); // 1cm std on x,y
 graph.add(PriorFactor<Pose2>(1, Pose2(0.0, 0.0, 1.57), priorNoise));

-------------------------------------------------------------------
Here is the code I tested with, compared to LocalizationExample.cpp, a prior node is added and also initialEstimate and UnaryFactor are updated.

#include <gtsam/geometry/Pose2.h>
#include <gtsam/inference/Key.h>
#include <gtsam/slam/BetweenFactor.h>
#include <gtsam/nonlinear/NonlinearFactorGraph.h>
#include <gtsam/nonlinear/Values.h>
#include <gtsam/nonlinear/LevenbergMarquardtOptimizer.h>
#include <gtsam/nonlinear/Marginals.h>

using namespace std;
using namespace gtsam;

class UnaryFactor : public NoiseModelFactor1<Pose2>
{
    // The factor will hold a measurement consisting of an (X,Y) location
    // We could this with a Point2 but here we just use two doubles
    double mx_, my_;

public:
    /// shorthand for a smart pointer to a factor
    typedef boost::shared_ptr<UnaryFactor> shared_ptr;

    // The constructor requires the variable key, the (X, Y) measurement value, and the noise model
    UnaryFactor(Key j, double x, double y, const SharedNoiseModel &model)
            : NoiseModelFactor1<Pose2>(model, j), mx_(x), my_(y)
    {
    }

    ~UnaryFactor() override
    {
    }

    // Using the NoiseModelFactor1 base class there are two functions that must be overridden.
    // The first is the 'evaluateError' function. This function implements the desired measurement
    // function, returning a vector of errors when evaluated at the provided variable value. It
    // must also calculate the Jacobians for this measurement function, if requested.
    Vector evaluateError(const Pose2 &q, boost::optional<Matrix &> H = boost::none) const override
    {
        // The measurement function for a GPS-like measurement is simple:
        // error_x = pose.x - measurement.x
        // error_y = pose.y - measurement.y
        // Consequently, the Jacobians are:
        // [ derror_x/dx  derror_x/dy  derror_x/dtheta ] = [1 0 0]
        // [ derror_y/dx  derror_y/dy  derror_y/dtheta ] = [0 1 0]
        if (H)
            (*H) = (Matrix(2, 3) << 1.0, 0.0, 0.0, 0.0, 1.0, 0.0).finished();
        return (Vector(2) << q.x() - mx_, q.y() - my_).finished();
    }

    // The second is a 'clone' function that allows the factor to be copied. Under most
    // circumstances, the following code that employs the default copy constructor should
    // work fine.
    gtsam::NonlinearFactor::shared_ptr clone() const override
    {
        return boost::static_pointer_cast<gtsam::NonlinearFactor>(
                gtsam::NonlinearFactor::shared_ptr(new UnaryFactor(*this)));
    }

    // Additionally, we encourage you the use of unit testing your custom factors,
    // (as all GTSAM factors are), in which you would need an equals and print, to satisfy the
    // GTSAM_CONCEPT_TESTABLE_INST(T) defined in Testable.h, but these are not needed below.
}; // UnaryFactor

int main(int argc, char** argv) {
    // 1. Create a factor graph container and add factors to it
    NonlinearFactorGraph graph;

    // Add prior node with 90 deg heading
    auto priorNoise = noiseModel::Diagonal::Sigmas(Vector3(0.01, 0.01, 0.1)); // 1cm std on x,y
    graph.add(PriorFactor<Pose2>(1, Pose2(0.0, 0.0, 1.57), priorNoise));

    // 2a. Add odometry factors
    // For simplicity, we will use the same noise model for each odometry factor
    auto odometryNoise = noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
    // Create odometry (Between) factors between consecutive poses
    graph.emplace_shared<BetweenFactor<Pose2> >(1, 2, Pose2(2.0, 0.0, 0.0), odometryNoise);
    graph.emplace_shared<BetweenFactor<Pose2> >(2, 3, Pose2(2.0, 0.0, 0.0), odometryNoise);

    // 2b. Add "GPS-like" measurements
    // We will use our custom UnaryFactor for this.
    auto unaryNoise = noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1));  // 10cm std on x,y
    graph.emplace_shared<UnaryFactor>(1, 0.0, 0.0, unaryNoise);
    graph.emplace_shared<UnaryFactor>(2, 0.0, 2.0, unaryNoise);
    graph.emplace_shared<UnaryFactor>(3, 0.0, 4.0, unaryNoise);
    graph.print("\nFactor Graph:\n");  // print

    // 3. Create the data structure to hold the initialEstimate estimate to the solution
    // For illustrative purposes, these have been deliberately set to incorrect values
    Values initialEstimate;
    initialEstimate.insert(1, Pose2(0.0, 0.5, 0.2));
    initialEstimate.insert(2, Pose2(0.1, 2.3, -0.2));
    initialEstimate.insert(3, Pose2(0.1, 4.1, 0.1));
    initialEstimate.print("\nInitial Estimate:\n");  // print

    // 4. Optimize using Levenberg-Marquardt optimization. The optimizer
    // accepts an optional set of configuration parameters, controlling
    // things like convergence criteria, the type of linear system solver
    // to use, and the amount of information displayed during optimization.
    // Here we will use the default set of parameters.  See the
    // documentation for the full set of parameters.
    LevenbergMarquardtOptimizer optimizer(graph, initialEstimate);
    Values result = optimizer.optimize();
    result.print("Final Result:\n");

    // 5. Calculate and print marginal covariances for all variables
    Marginals marginals(graph, result);
    cout << "x1 covariance:\n" << marginals.marginalCovariance(1) << endl;
    cout << "x2 covariance:\n" << marginals.marginalCovariance(2) << endl;
    cout << "x3 covariance:\n" << marginals.marginalCovariance(3) << endl;

    return 0;
}

-------------------------------------------------------------------
Here is the print out when setting the verbosity to "ERROR":

Factor Graph:
size: 6
Factor 0: PriorFactor on X1
  prior mean: (0, 0, 1.57)
  noise model: diagonal sigmas[0.01; 0.01; 0.1];
Factor 1: BetweenFactor(X1,X2)
  measured: (2, 0, 0)
  noise model: diagonal sigmas[0.2; 0.2; 0.1];
Factor 2: BetweenFactor(X2,X3)
  measured: (2, 0, 0)
  noise model: diagonal sigmas[0.2; 0.2; 0.1];
Factor 3:   keys = { X1 }
isotropic dim=2 sigma=0.1
Factor 4:   keys = { X2 }
isotropic dim=2 sigma=0.1
Factor 5:   keys = { X3 }
isotropic dim=2 sigma=0.1

Initial Estimate:
Values with 3 values:
Value X1: (gtsam::Pose2) (0, 0.5, 0.2)
Value X2: (gtsam::Pose2) (0.1, 2.3, -0.2)
Value X3: (gtsam::Pose2) (0.1, 4.1, 0.1)

Initial error: 1551.06967
newError: 23.1575862
errorThreshold: 23.1575862 > 0
absoluteDecrease: 1527.91208091 >= 1e-05
relativeDecrease: 0.985069925166 >= 1e-05
newError: 10.6598349889
errorThreshold: 10.6598349889 > 0
absoluteDecrease: 12.497751214 >= 1e-05
relativeDecrease: 0.539682810831 >= 1e-05
newError: 10.6557111698
errorThreshold: 10.6557111698 > 0
absoluteDecrease: 0.00412381900708 >= 1e-05
relativeDecrease: 0.000386855801369 >= 1e-05
newError: 10.6526461044
errorThreshold: 10.6526461044 > 0
absoluteDecrease: 0.00306506546349 >= 1e-05
relativeDecrease: 0.000287645321334 >= 1e-05
newError: 10.650195516
errorThreshold: 10.650195516 > 0
absoluteDecrease: 0.00245058839893 >= 1e-05
relativeDecrease: 0.000230045039975 >= 1e-05
newError: 10.6482371651
errorThreshold: 10.6482371651 > 0
absoluteDecrease: 0.00195835089971 >= 1e-05
relativeDecrease: 0.000183879337874 >= 1e-05
newError: 10.6467302295
errorThreshold: 10.6467302295 > 0
absoluteDecrease: 0.00150693554209 >= 1e-05
relativeDecrease: 0.000141519719999 >= 1e-05
newError: 10.6456548513
errorThreshold: 10.6456548513 > 0
absoluteDecrease: 0.00107537822662 >= 1e-05
relativeDecrease: 0.00010100549215 >= 1e-05
newError: 10.6449969812
errorThreshold: 10.6449969812 > 0
absoluteDecrease: 0.000657870132359 >= 1e-05
relativeDecrease: 6.17970563152e-05 >= 1e-05
newError: 10.6447445791
errorThreshold: 10.6447445791 > 0
absoluteDecrease: 0.000252402130714 >= 1e-05
relativeDecrease: 2.3710869168e-05 >= 1e-05
Warning:  Levenberg-Marquardt giving up because cannot decrease error with maximum lambda
newError: 10.6447445791
errorThreshold: 10.6447445791 > 0
absoluteDecrease: 0 < 1e-05
relativeDecrease: 0 < 1e-05
converged
errorThreshold: 10.6447445791 <? 0
absoluteDecrease: 0 <? 1e-05
relativeDecrease: 0 <? 1e-05
iterations: 10 >? 100
Final Result:
Values with 3 values:
Value X1: (gtsam::Pose2) (-0.000165560745219, 3.35236062356e-05, 1.63615758698)
Value X2: (gtsam::Pose2) (-0.196865810578, 2.0110305545, 1.66201771231)
Value X3: (gtsam::Pose2) (-0.369991575177, 3.84331941327, 1.66405643419)

Expected behavior

gtsam should converge to the GPS positions as shown in the below figure plotted by Matlab gtsam-toolbox-3.2.0-win64:

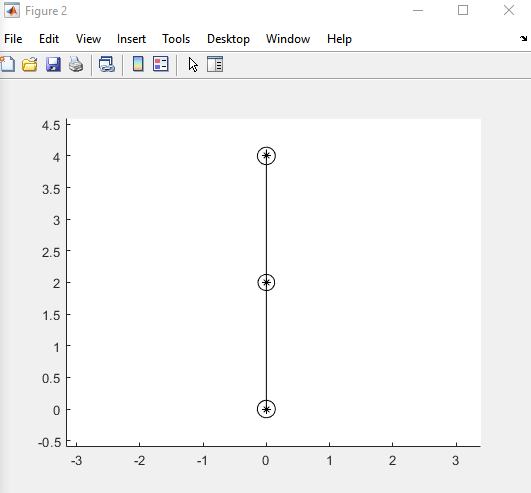
However the c++ solutions look like the green dots in the following picture:

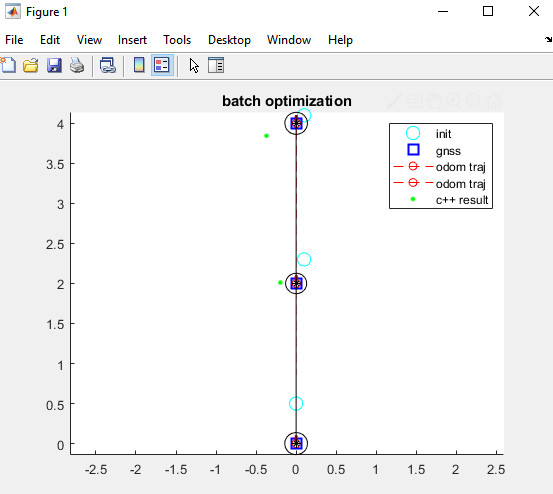
Environment

We have used C++ as the language together with gtsam 4.0.3 in Ubuntu 18.04. Matlab gtsam-toolbox-3.2.0-win64 is used for simulations and plotting. Note that in Matlab PriorFactorPose2 is used as the equivalent for the UnaryFactor in C++ since we did not figured how to add a custom factor in Matlab. So the comparison of the results between Matlab and C++ is not entirely fair but C++ is expected to give decent results.

Additional information

[dellaert]

Did you init test your derivatives? Numerous examples to do this with numerical differentiation. Or use the super-handy EXPECT_CORRECT_FACTOR_JACOBIANSin factorTesting.h

[nmahabadi]

For this test I used the original UnaryFactor class from the LocalizationExample.cpp

if (H)  (*H) = (Matrix(2, 3) << 1.0, 0.0, 0.0, 0.0, 1.0, 0.0).finished();
return (Vector(2) << q.x() - mx_, q.y() - my_).finished();

The Jacobian is definitely correct for the given error function, however the question is if the formulated error function is valid. As shown by the results of the test case, the optimizer cannot converge to the solutions...

[dellaert]

I'm not so convinced about the Jacobian. How about quickly calling EXPECT_CORRECT_FACTOR_JACOBIANS now that you have everything set up? We might be surprised, as Jacobian is about the tangent space on the right.

[nmahabadi]

I didn't manage to get the EXPECT_CORRECT_FACTOR_JACOBIANS working, probably something do to with conan recipe which I am working on. But for the time being I used testFactorJacobians from <factorTesting.h> directly.
I tested to cases; one with no orientation and the other with 90° orientation:

1. No orientation:

Key           poseKey(1);
Values values;
values.insert(poseKey, Pose2(2.0, 0.0, 0.0));
auto         noise = noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1));
Pose2        measurement(2.1, 0.0, 0.0);
UnaryFactor factor(poseKey, measurement.x(), measurement.y(), noise);
std::cout << gtsam::internal::testFactorJacobians("dummy", factor, values, 1e-7, 1e-4) << std::endl;

result: this is ok since testFactorJacobians returns true.

2. 90° orientation:
values.insert(poseKey, Pose2(2.0, 0.0, 1.57));
result: the Jacobian is not correct when there is an orientation:

Not equal:
expected:
A[1] = [
0.00796327 -10 0;
10 0.00796327 0
]
b = [ 1 -0 ]
No noise model
actual:
A[1] = [
10 0 0;
0 10 0
]
b = [ 1 -0 ]
No noise model
not equal:
expected = [
0.00796327, -10, 0;
10, 0.00796327, 0
]
actual = [
10, 0, 0;
0, 10, 0
]
actual - expected = [
9.99204, 10, 0;
-10, 9.99204, 0
]
Mismatch in Jacobian 1 (base 1), as shown above

[nmahabadi]

It seems that the expected Jacobian is as follows:
H = [R 0]
with R as the rotation matrix.

[dellaert]

Indeed, this is what I suspected :-) Try correcting the factor and see whether everything works? If so, a PR with the change would be much appreciated.

[nmahabadi]

I tested the factor with correct Jacobian and it seems to be working perfect with real data as well as synthetic ones. I will send a PR, but for my understanding gtsam expect to have error and Jacobian in tangent space right?

[nmahabadi]

This is the PR for fixing the Jacobian:
#715

I think as an improvement, we can have UnaryFactor class as a stand-alone factor.