For a better understanding of the examples in Structure and Interpretation of Computer Programs(SICP), as well as learning Emacs lisp, exercises will be answered in Scheme or Elisp.
MIT Version:
https://mitpress.mit.edu/sites/default/files/sicp/full-text/book/book-Z-H-23.html#%_sec_3.4
Online Version:
https://sarabander.github.io/sicp/html/4_002e2.xhtml#g_t4_002e2
SICP Interactive Version:
https://xuanji.appspot.com/isicp/index.html
Berkeley Python Version:
https://inst.eecs.berkeley.edu/~cs61a/sp12/book/index.html
https://composingprograms.com/
Interactive Javascript Version:
https://sourceacademy.org/sicpjs
Racket SICP collections:
https://docs.racket-lang.org/sicp-manual/
Racket SICP Picture language (used in Chapter 2.2):
https://docs.racket-lang.org/sicp-manual/SICP_Picture_Language.html
Emacs lisp evaluation:
https://www.gnu.org/software/emacs/manual/html_node/efaq/Evaluating-Emacs-Lisp-code.html
NOTE 1: Emacs do not have the optimization of tail recursion according to this SO answer, we need to increase the default max-lisp-eval-depth, otherwise we'll run into errors easily.
Add the following lines to .emacs:
;; increase max-lisp-eval-depth from 500 to 100000
(setq max-specpdl-size 100000
max-lisp-eval-depth 100000)
NOTE 2: Add (setq lexical-binding t) to the buffer to enable Elisp closure, see lexical bidning.
The discussion in this section about the difference between recursion and iteration is a must-read, and priceless.
Iterative process: the program variables provide a complete description of the state of the process at any point. If we stopped the computation between steps, all we would need to do to resume the computation is to supply the interpreter with the values of the three program variables.
Recursive process: there is some additional “hidden” information, maintained by the interpreter and not contained in the program variables, which indicates “where the process is” in negotiating the chain of deferred operations. The longer the chain, the more information must be maintained.
Recursive procedure: the syntactic fact that the procedure definition refers (either directly or indirectly) to the procedure itself.
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
(define (fact-iter product counter max-count)
(if (> counter max-count)
product
(fact-iter (* counter product)
(+ counter 1)
max-count)))
factorial is a linear recursive process (it has hidden information) and a recursive procedure (it calls itself directly). The call stack of procedure grows and shrinks.
fact-iter is an iterative process (no hidden information, product, counter and max-count contain the complete state) and a recursive procedure (it calls itself directly). The call stack of procedure does not grow and shrink with tail-recursive implementation.
For common languages (C, Python) that do not implement tail recursion, describe iterative process only by resorting to special-purpose “looping constructs” such as do, repeat, until, for, and while.
The Scheme interpreter implements tail recursion, so the special iteration constructs are useful only as syntactic sugar.
Higher-order procedures are procedures that manipulate procedures that accept procedures as arguments or return procedures as values.
Quote from the book:
Yet even in numerical processing we will be severely limited in our ability to create abstractions if we are restricted to procedures whose parameters must be numbers. Often the same programming pattern will be used with several different procedures.
To eliminate the definition of trivial procedures in higher-order procedures, lambda is introduced to define procedures on the fly.
By the way, the name lambda is a bit obscure, it would be clearer and less intimidating to people learning Lisp if a name more obvious than lambda, such as make-procedure, were used.
Quote from the book:
In general, programming languages impose restrictions on the ways in which computational elements can be manipulated. Elements with the fewest restrictions are said to have first-class status. Some of the “rights and privileges” of first-class elements are:
- They may be named by variables.
- They may be passed as arguments to procedures.
- They may be returned as the results of procedures.
- They may be included in data structures.65
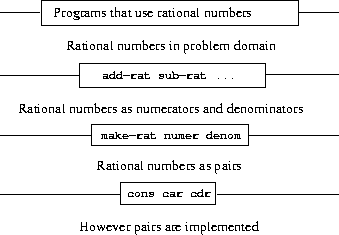
Just like procedure abstraction, data abstraction is a methodology that enables us to isolate how compound data is used from the details of how it is constructed.
As the example of rational numbers demonstrates,
lower layers expose only a few methods (constructor & selectors ) for the upper layers to use, how the lower layers are implemented is irrelevant to the upper layer.
A valid but counter-intuitive implementation of cons:
(define (cons x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argument not 0 or 1 -- CONS" m))))
dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1))
In general, we can think of data as defined by some collection of selectors and constructors, together with specified conditions that these procedures must fulfill in order to be a valid representation.
This definition does not distinguish whether Data is a "real" data structure or not, as long as it satisfies the conditions.
The "closure property" of cons, meaning, the result of cons can be combined using cons again. It permits us to create "sequences" and "hierarchical" structures (List, Tree).
The use of the word "closure" here comes from abstract algebra, where a set of elements is said to be closed under an operation if applying the operation to elements in the set produces an element that is again an element of the set. The Lisp community also (unfortunately) uses the word "closure" to describe a totally unrelated concept: A closure is an implementation technique for representing procedures with free variables. We do not use the word "closure" in this second sense in this book.
The examples in this section demonstrate two powerful design principles, "conventional interfaces" and "stratified design".
(define (salary-of-highest-paid-programmer records)
(accumulate max
0
(map salary
(filter programmer? records))))
Sequences, implemented here as lists, serve as a conventional interface that permits us to combine processing modules.
The picture language demonstrates the power of stratified design in a complex system. Just like data abstraction barriers in section 2.1, the picture language uses primitive painters segments->painter, combines those primitive painters to geometric combiners such as beside and below, then uses those combiners as primitives to work at a higher level, such as square-of-four.
Stratified design helps make programs robust, that is, it makes it likely that small changes in a specification will require correspondingly small changes in the program.
Symbolic data has a quotation mark ' at the beginning of the object, which is used to represent arbitrary symbols as data, e.g, '+, '-, '*, '/.
From the interpreter's point of view, everything in the Lisp is a list, quotation mark is just a single-character abbreviation for wrapping the next complete expression with a quote to form (quote <expression>).
A quotation can also be placed to compound objects, e.g. '(+ 1 2), that represents a list. Quote an empty list '() represents as nil.
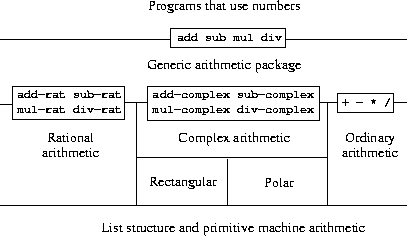
Abstraction barriers in section 2.1 are "horizontal", lower level implementations that can be replaced without affecting the upper level.
This section introduces "vertical" barriers, which are used to separate data that have multiple representations.
As the example of the complex-arithmetic package demonstrates, a new representation can be added without affecting the usage of the upper level.
Each representation of data has its constructor and a "special tag" which is used to distinguish what type of data is.
For example, Ben's rectangular representation:
(cons 'rectanular (cons 3 4))
Alyssa's polar representation:
(cons 'polar (cons 3 4))
Generic interfaces such as real-part, imag-part, magnitude, angle will check the type of data, and dispatch the corresponding selector procedure.
(define (real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
(else (error "Unknown type -- REAL-PART" z))))
The dispatching on type strategy is a powerful strategy for obtaining modularity in system design. But it has two weaknesses:
-
Generic selector such as
real-parthas to know about all the different representations. -
Individual representations may have name conflicts, so it needs to be named like
real-part-rectangularandreal-part-polar.
The issue underlying both of these weaknesses is that the technique for implementing generic interfaces is not
additive.
Data-directed programming uses an "operation-type" table to make generic interfaces additive. To add a new representation, we need only add new entries to the table and the interfaces remain intact.
The table is stored in a data structure similar to the hash table, with the put and get procedures.
(define (install-rectangular-package)
...
(put 'real-part '(rectangular) real-part)
)
(define (install-polar-package)
...
(put 'real-part '(polar) real-part)
)
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(error
"No method for these types -- APPLY-GENERIC"
(list op type-tags))))))
(define (real-part z) (apply-generic 'real-part z))
An alternative implementation strategy is to decompose the table into columns and, instead of using "intelligent operations" that dispatch on data types, work with "intelligent data objects" that dispatch on operation names.
(define (make-from-real-imag x y)
(define (dispatch op)
(cond ((eq? op 'real-part) x)
((eq? op 'imag-part) y)
((eq? op 'magnitude)
(sqrt (+ (square x) (square y))))
((eq? op 'angle) (atan y x))
(else
(error "Unknown op -- MAKE-FROM-REAL-IMAG" op))))
dispatch)
(define (apply-generic op arg) (arg op))
(define (real-part z) (apply-generic 'real-part z))
This strategy is similar to the method call in object-oriented programming and will be detailed explained in detail in Chapter 3.
Generic operations in section 2.4 mainly focused on different representations of the same type of data. In this section, generic operations can be further applied to different types of data.
Consider the addition of complex number to an ordinary number (add <complex-number> <scheme-number>).
One way to handle this is to design a procedure for each possible combination of types. For example,
;; to be included in the complex package
(define (add-complex-to-schemenum z x)
(make-from-real-imag (+ (real-part z) x)
(imag-part z)))
(put 'add '(complex scheme-number)
(lambda (z x) (tag (add-complex-to-schemenum z x))))
This technique works, but it is cumbersome and does not scale if we have several types of data (e.g. rational number, real number, complex number...).
Since those types are not completely independent, scheme numbers can be converted to rational numbers which can be converted to real numbers and further to complex numbers. This process is called coercion.
We can define the following converter procedure:
(define (scheme-number->complex n)
(make-complex-from-real-imag (contents n) 0))
(put-coercion 'scheme-number 'complex scheme-number->complex)
and put it to a hash table, then modify the apply-genric procedure to look up this table if no procedure is found in the previous operation-type table.
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags))))))
(error "No method for these types"
(list op type-tags)))))))
From this chapter, we view the world as the composition of many objects, each object has its local state variables, and objects can interact with each other. Since the states of objects change over time, an assignment operator` must be provided by the language.
We can use let to establish an environment with a local state variable, and use set! to mutate the local state.
(define new-withdraw
(let ((balance 100))
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))))
The benefit of introducing assignments is that we can structure systems in a more modular fashion than if all states had to be manipulated explicitly by passing additional parameters.
The cost of introducing an assignment is that our programming language can no longer be interpreted in terms of the substitution model.
Programming without using any assignments, as we did throughout the first two chapters. The same procedure with the same arguments will always produce the same result so that procedures can be viewed as computing mathematical functions, thus the name "functional".
Programming that makes extensive use of assignment, which makes our computation model complicated which we will see in section 3.2. Programs written in imperative style are susceptible to bugs that cannot occur in functional programs. It becomes even worse if we consider applications in which several processes execute concurrently which we will see in section 3.4.
In view of this, it is ironic that introductory programming is most often taught in a highly imperative style. This may be a vestige of a belief, common throughout the 1960s and 1970s, that programs that call procedures must inherently be less efficient than programs that perform assignments. (Steele (1977) debunks this argument.) Alternatively it may reflect a view that step-by-step assignment is easier for beginners to visualize than procedure call. Whatever the reason, it often saddles beginning programmers with "should I set this variable before or after that one" concerns that can complicate programming and obscure the important ideas.
This section is very important and worth reading more than once.
The environment is crucial to the evaluation process because it determines the context in which an expression should be evaluated.
An environment is a series of frames. Frame, like a box or a set, may contain several bindings, which associate variable names with their corresponding values.
In the environment model of evaluation, a procedure object is always a pair consisting of some code and a pointer to an environment, e.g. (cons <func-params and body> <env pointer>).
For example,
(define (square x)
(* x x))
When a procedure is defined, the lambda expression was evaluated to produce the procedure, and a new binding, which associates the procedure object with the symbol square, has been added to the global environment.
When the procedure is applied, (square 5), a new frame was created and binds the parameters x to the value 5. Within this new environment, we evaluate the body of square (* x x), and the result is (* 5 5), or 25.
Another example,
(define (f x)
(define (g y)
(+ x y))
g)
When f is defined, a new procedure object is created and a new symbol f is created in the global environment which binds to the newly created procedure object.
When f is applied, (f 5), a new frame containing x=5 is created. Within this new environment, we start to evaluate the body of f which defines another function g. Again, a new procedure object is created and a new symbol g is created in the environment where f is evaluated, and bound to the newly created procedure object.
When g is applied, ((f 5) 6), a new frame containing y=6 is created and points to the previous frame containing x=5, within this new environment, we start to evaluate the body of g (+ x y), and the result is (+ 5 6), or 11.
The crucial point to observe is that the frame created by g has its enclosing environment, not the global environment, but rather the environment used by f.
The environment model of procedure application can be summarized by two rules:
A procedure object is applied to a set of arguments by constructing a frame, binding the formal parameters of the procedure to the arguments of the call, and then evaluating the body of the procedure in the context of the new environment constructed. The new frame has as its enclosing environment the environment part of the procedure object being applied.
A procedure is created by evaluating a lambda expression relative to a given environment. The resulting procedure object is a pair consisting of the text of the lambda expression and a pointer to the environment in which the procedure was created.
These rules, though considerably more complex than the substitution model, are still reasonably straightforward.
Applying the same procedure multiple times will create different frames, the set! operator in the procedure only mutates the value in its frame.
To model systems composed of objects that have changing states, mutators are introduced in this section. These mutators greatly enhance the representational power of pairs, enabling us to build more complex data structures like queues and tables.
Two examples (simulator for digital circuits and constraints propagation system) in this section are fascinating and eye-opening.
This section goes further in structuring computational models to match our perception of the physical world. Objects act concurrently, the states do not change at a time in sequence, but all at once.
Serializer can be used to control access to shared variables.
The following code can only produce only two possible values for x, 101, or 121. The other possibilities are eliminated because the execution of P1 and P2 cannot be interleaved.
(define x 10)
(define s (make-serializer))
(parallel-execute (s (lambda () (set! x (* x x))))
(s (lambda () (set! x (+ x 1)))))
Serializers can be implemented in terms of a more primitive synchronization mechanism called a mutex.
(define (make-serializer)
(let ((mutex (make-mutex)))
(lambda (p)
(define (serialized-p . args)
(mutex 'acquire)
(let ((val (apply p args)))
(mutex 'release)
val))
serialized-p)))
A mutex is a mutable object that can hold the value true or false. When the value is false, the mutex is available to be acquired. When the value is true, the mutex is unavailable, and any process that attempts to acquire the mutex must wait.
(define (make-mutex)
(let ((cell (list false)))
(define (the-mutex m)
(cond ((eq? m 'acquire)
(if (test-and-set! cell)
(the-mutex 'acquire))) ; retry
((eq? m 'release) (clear! cell))))
the-mutex))
(define (clear! cell)
(set-car! cell false))
The test-and-set! operation must be performed atomically. Following implementation does not suffice.
(define (test-and-set! cell)
(if (car cell)
true
(begin (set-car! cell true)
false)))
The actual implementation of test-and-set! depends on the details of how our system runs concurrent processes.
For example, for a sequential processor using a time-slicing mechanism, test-and-set! can work by disabling time-slicing during the testing and setting. Alternatively, multiprocessing computers provide instructions that support atomic operations directly in hardware.
Deadlock is always a danger in systems that provide concurrent access to multiple shared resources.
One way to avoid the deadlock in this situation is to give each account a unique identification number and rewrite serialized-exchange so that a process will always attempt to enter a procedure protecting the lowest-numbered account first.
In an attempt to model real-world phenomena, we made some apparently reasonable decisions: We modeled real-world objects with local state by computational objects with local variables. We identified time variation in the real world with time variation in the computer. We implemented the time variation of the states of the model objects in the computer with assignments to the local variables of the model objects.
Using objects with local states to model the real-world and change states over time using set! will raise some complex problems in some circumstances like concurrency.
We can use streams to model the change of states without using set!. The initial value and the value after each change are stored in a sequence-like data structure called streams. We can refer to the state at any time in the stream, a stream can be very large (even infinite).
Streams can be implemented using a "delayed list".
A delayed list likes a normal list '(1 2 3), except the cdr of the list is delayed evaluated.
We can make a delayed list using cons-stream, which is a special form defined so that
(cons-stream <a> <b>)
is equivalent to
(cons <a> (delay <b>))
We can use the macro to implement cons-stream as:
(define-syntax cons-stream
(syntax-rules ()
((cons-stream a b)
(cons a (delay b)))))
When the cdr of a stream is referred, it's then forced to evaluate.
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
A stream has all the operations that a list has, like stream-ref, stream-for-each, stream-map, stream-filter ...
Delay can be a special form such that
(delay <exp>)
is syntactic sugar for
(lambda () <exp>)
We can use macros to implement delay as:
(define-syntax delay
(syntax-rules ()
((delay exp)
(memo-proc (lambda () exp)))))
Force simply calls the procedure (of no arguments) produced by delay, so we can implement force as a procedure:
(define (force delayed-object)
(delayed-object))
An important optimization that should be introduced to the delay function is the memo-proc function which is used to remember the previous calculated value in the stream.
(define (memo-proc proc)
(let ((already-run? false) (result false))
(lambda ()
(if (not already-run?)
(begin (set! result (proc))
(set! already-run? true)
result)
result))))
An infinite integer can be defined by specifying a generating procedure that explicitly computes the stream elements one by one:
(define (integers-starting-from n)
(cons-stream n (integers-starting-from (+ n 1))))
(define integers (integers-starting-from 1))
The car of integers is 1 and the cdr is a promise to produce the integers beginning with 2.
A stream can also be implicitly defined like a recursive procedure:
(define ones (cons-stream 1 ones))
ones is a pair whose car is 1 and whose cdr is a promise to evaluate ones. Evaluating the cdr gives us again a 1 and a promise to evaluate ones, and so on.
Together with add-streams, we can define integers as:
(define integers (cons-stream 1 (add-streams ones integers)))
This defines integers to be a stream whose first element is 1 and the rest of which is the sum of ones and integers.
The stream approach can be illuminating because it allows us to build systems with different module boundaries than systems organized around assignment to state variables. For example, we can think of an entire time series (or signal) as a focus of interest, rather than the values of the state variables at individual moments. This makes it convenient to combine and compare components of state from different moments.
Modeling with streams is not as intuitive as modeling with objects, largely because the latter matches the perception of interacting with a world of which we are part.
Delayed evaluation and assignment don't mix well. As footnote #59 states,
Part of the power of stream processing is that it lets us ignore the order in which events actually happen in our programs. Unfortunately, this is precisely what we cannot afford to do in the presence of assignment, which forces us to be concerned with time and change.
In this section, we are using Lisp to construct an evaluator that can evaluate Lisp program, this is called Meta-circurlar Evaluator.
The environment model in section 3.2 has two basic parts:
-
To evaluate a combination (a compound expression other than a special form), evaluate the subexpressions and then apply the value of the operator subexpression to the values of the operand subexpressions.
-
To apply a compound procedure to a set of arguments, evaluate the body of the procedure in a new environment. To construct this environment, extend the environment part of the procedure object by a frame in which the formal parameters of the procedure are bound to the arguments to which the procedure is applied.
The metacircular evaluator is essentially a Scheme formulation of the environment model of evaluation.
Two critical procedures in the evaluator are eval and apply.
eval takes as arguments an expression and an environment. It classifies the expression into three kinds:
-
primitive expressions
-
self-evaluating expressions, the only self-evaluating items are numbers and strings.
-
variables which values will be found in the environment, e.g.
a,f
-
-
special forms
-
quote, e.g.
(quote a) -
assignment, e.g.
(set! <variable> <value>) -
if, e.g
(if <predicate> <consequent> <alternative>) -
lambda, e.g
(lambda (<args>) <BODY>) -
begin, e.g
(begin <exp1> <exp2> ... <expN>) -
cond, e.g
(cond (<predicate1> <exp1>) ... (<predicateN> <expN>) (else <exp>))
-
-
combinations (compound expressions), e.g.
(+ 1 1) (fib 3)recursively call
evalon operator and operands, the resulting procedure and arguments are passed toapply.
apply takes two arguments, a procedure and a list of arguments. It classifies the procedure into two kinds:
-
primitive procedures, e.g.
+ - * / =just call the underlying Scheme procedures.
-
compound procedures, e.g.
fib squaresequentially call
evalon the expressions that make up the procedure body.
eval and apply are mutual recursive, as the following picture shows:
The value of metaevaluator is that we can experiment with alternative choices in language design simply by modifying the evaluator.
The default evaluation order of Scheme is Applicative Order which means evaluating all the arguments when a procedure is applied.
Another evaluation order is Normal Order which means delay evaluation of procedure arguments until the actual argument values are needed.
Delaying evaluation of procedure arguments until the last possible moment (e.g., until they are required by a primitive operation) is called lazy evaluation.
Thunk is past tense of "think" in informal occations as stated in this Quora thread.
The word thunk was invented by an informal working group that was discussing the implementation of call-by-name in Algol 60. They observed that most of the analysis of ("thinking about") the expression could be done at compile time; thus, at run time, the expression would already have been "thunk" about (Ingerman et al. 1960).
- create a thunk by
delay-it
(define (delay-it exp env)
(list 'thunk exp env))
(define (thunk? obj)
(tagged-list? obj 'thunk))
(define (thunk-exp thunk) (cadr thunk))
(define (thunk-env thunk) (caddr thunk))
- evaluate a thunk by
force-it
(define (actual-value exp env)
(force-it (eval exp env)))
(define (force-it obj)
(if (thunk? obj)
(actual-value (thunk-exp obj) (thunk-env obj))
obj))
Interaction between lazy evaluation and side effects can be very confusing.
Using lazy evaluation, we can get rid of cons-stream and stream- related operations in section 3.5, the arguemnts of (cons a b) are delay evaluated until they are actually used by some primitive procedures. Thus, all lists are delayed.
And further more, the car of a cons is also delay evaluted, this feature permits us to create delayed versions of more general kinds of list structures, not just sequences. Such as lazy trees which is discussed in the paper by Hughes. Lazy trees can represent all possible positions a game can reach -- and this is used to evaluate potential moves in games like chess.
In this section, we are designing a register matchine to gain more complete understanding of the underlying Lisp system.
The metaevaluator in Chapter 4 leaves important questions unanswered. For instance, how the evaluation of subexpression manages to return a value to the expression that uses this value? How some recursive procedures generate iterative processes whereas others generate recursive processes?
We will design our own machine language instead of focusing on the machine language of any particular computer. Here are the views of authors of the book,
Our descriptions of processes executed by register machines will look very much like “machine-language” programs for traditional computers. However, instead of focusing on the machine language of any particular computer, we will examine several Lisp procedures and design a specific register machine to execute each procedure. Thus, we will approach our task from the perspective of a hardware architect rather than that of a machine-language computer programmer.
Register: has a name and the buttons that control assignment to it.
Register button: has a name and the source(a register, a cosntant, or an operation) of data that enters the reigster.
Operation: has a name and inputs(registers or constants), operate directly only on constants and the contents of registers, not on the results of other operations.
Controller of a matchine: as a sequence of instructions together with labels that identify entry points in the sequence.
An instruction is one of the following:
-
The name of a data-path button to push to assign a value to a register. (is corresponds to a box in the controller diagram.)
-
A test instruction.
-
A conditional branch (branch instruction) to a location indicated by a controller label, based on the result of the previous test.
-
An unconditional branch (goto instruction) naming a controller label at which to continue execution.
For example, The GCD procedure in Euclid's Algorithm:
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
The data paths and controller for a GCD machine:
The corresponding GCD machine is described as follows:
(define-machine gcd
;; Purpose: (assign a gcd (fetch a) (fetch b)))
;; Side effect is to set contents of b to zero.
;; First we declare our data paths.
(registers a b t1) ;These are the registers we may use.
(operations ;These are the operations we may use.
(assign tl (remainder (fetch a) (fetch b)))
(assign a (fetch b))
(assign b (fetch t1))
(branch (zero? (fetch b)) gcd-done)
(goto test-b))
;; This is the program for the controller.
(controller
test-b ;This is a label
(branch (zero? (fetch b)) gcd-done)
(assign t1 (remainder (fetch a) (fetch b)))
(assign a (fetch b))
(assign b (fetch t1))
(goto test-b) ;Continue at label above
gcd-done))
There are two kind of special operations: Read and Print.
-
Read: takes inputs from something outside of the machine and stores to a register.
-
Print: printing the contents of a register.
(perform (op print) (reg a))
In order to hold one copy of the GCD routine and reuse registers(a b t1) between multiple GCDs, another register continue is introduced to hold continuation information.
Before calling gcd, the label after-gcd is saved into the continue. When gcd is done, goto the label in continue.
GCD subroutine:
gcd
...
gcd-done
(goto (reg continue))
Calling gcd-1 and gcd-2:
; calling gcd
(assign continue (label after-gcd-1))
(goto (label gcd))
after-gcd-1
...
; calling another gcd
(assign continue (label after-gcd-2))
(goto (label gcd))
after-gcd-2
This approach works well even if there are other subroutines, such as fact, sub in the machine, just make sure to save the continuation information before calling the subroutine.
However, if we have a subroutine (sub1) calling another subroutine (sub2), this approach will failed, since the contination information of sub1 will be overwritten by the sub2.
In order to implement subroutine calls, the content of continue must be saved in some place. These values must be restored in the reverse of the order in which they were saved, since the innermost subroutine call must return first.
Also, in order to implement recurive process, some values in the registers must be saved as well.
This dictates the use of a stack, or “last in, first out” data structure, to save register values.
For example, a recursive factorial procedure,
(controller
(assign continue (label fact-done)) ; set up final return address
fact-loop
(test (op =) (reg n) (const 1))
(branch (label base-case))
(save continue) ; Set up for the recursive call
(save n) ; by saving n and continue.
(assign n (op -) (reg n) (const 1)) ; Set up continue so that the
(assign continue (label after-fact)) ; computation will continue
(goto (label fact-loop)) ; at after-fact when the
after-fact ; subroutine returns.
(restore n)
(restore continue)
(assign val (op *) (reg n) (reg val)) ; val now contains n(n - 1)!
(goto (reg continue)) ; return to caller
base-case
(assign val (const 1)) ; base case: 1! = 1
(goto (reg continue)) ; return to caller
fact-done)
A controller instruction in our register-machine language has one of the following forms, where each ⟨ input i ⟩ is either (reg ⟨register-name⟩) or (const ⟨constant-value⟩). These instructions were introduced in 5.1.1:
(assign ⟨register-name⟩ (reg ⟨register-name⟩))
(assign ⟨register-name⟩
(const ⟨constant-value⟩))
(assign ⟨register-name⟩
(op ⟨operation-name⟩)
⟨input₁⟩ … ⟨inputₙ⟩)
(perform (op ⟨operation-name⟩)
⟨input₁⟩
…
⟨inputₙ⟩)
(test (op ⟨operation-name⟩)
⟨input₁⟩
…
⟨inputₙ⟩)
(branch (label ⟨label-name⟩))
(goto (label ⟨label-name⟩))
The use of registers to hold labels was introduced in 5.1.3:
(assign ⟨register-name⟩ (label ⟨label-name⟩))
(goto (reg ⟨register-name⟩))
Instructions to use the stack were introduced in 5.1.4:
(save ⟨register-name⟩)
(restore ⟨register-name⟩)