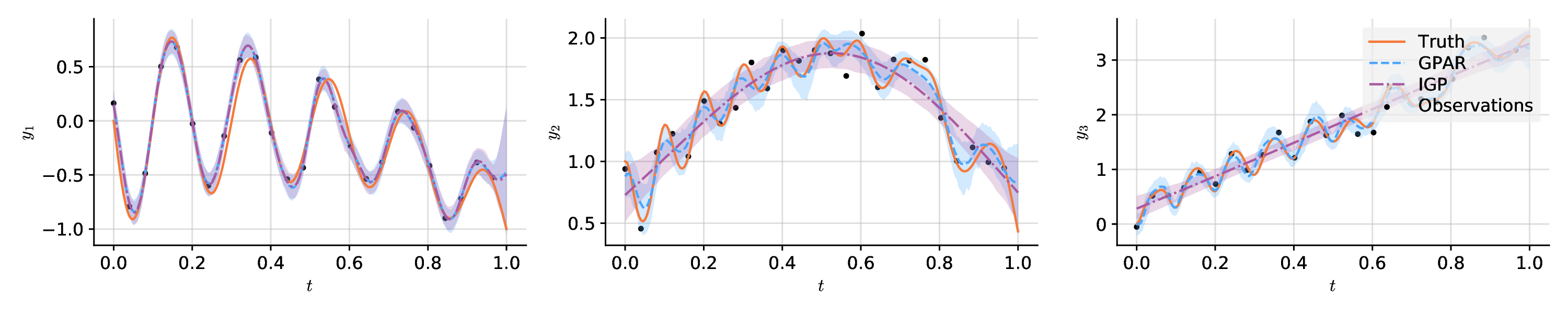
Implementation of the Gaussian Process Autoregressive Regression Model. See the paper, and see the docs.
pip install gpar
A simple instance of GPAR can be created as follows:
from gpar import GPARRegressor
gpar = GPARRegressor(
replace=True,
impute=True,
scale=1.0,
linear=True,
linear_scale=100.0,
nonlinear=True,
nonlinear_scale=1.0,
noise=0.1,
normalise_y=True
)Here the keyword arguments have the following meaning:
-
replace=True: Replace data points with the posterior mean of the previous layer before feeding them into the next layer. This helps the model deal with noisy data, but may discard important structure in the data if the fit is bad. -
impute=True: GPAR requires that data is closed downwards. If this is not the case, the model will be unable to use part of the data. SettingimputetoTruelets GPAR impute data points to ensure that the data is closed downwards. -
scale=1.0: Initialisation of the length scale with respect to the inputs. -
linear=True: Use linear dependencies between outputs. -
linear_scale=100.0: Initialisation of the length scale of the linear dependencies between outputs. -
nonlinear=True: Also use nonlinear dependencies between outputs. -
nonlinear_scale=1.0: Initialisation of the length scale of the nonlinear dependencies between outputs. Important: this length scale applies after possible normalisation of the outputs (see below), in which casenonlinear_scale=1.0corresponds to a simple, but nonlinear relationship. -
noise=0.1: Initialisation of the variance of the observation noise. -
normalise_y=True: Internally, work with a normalised version of the outputs by subtracting the mean and dividing by the standard deviation. Predictions will be transformed back appropriately.
In the above, any scalar hyperparameter may be replaced by a list of values
to initialise each layer separately, e.g. scale=[1.0, 2.0]. See the
documentation for a full overview of the keywords that may be passed to
GPARRegressor.
By default, GPAR models dependencies between outputs as follows:
-
the first output
y1is modelled as a function of only the inputsx:y1 = y1(x); -
the second output
y2is modelled as a function of the previous outputy1and the inputsx:y2 = y2(y1, x); -
the third output
y3is modelled as a function of the previous outputsy2andy1and the inputsx:y3 = y3(y2, y1, x); -
et cetera.
To fit GPAR, call gpar.fit(x_train, y_train) where x_train are the training
inputs and y_train the training outputs.
The inputs x_train must have shape (n,) or (n, m), where n is the
number of data points and m the number of input features, and the outputs
y_train must have shape (n,) or (n, p), where p is the number of
outputs.
Missing data can simply be set to np.nans.
To condition GPAR on data without optimising its hyperparameters, use
gpar.condition(x_train, y_train) instead.
Finally, to make predictions, call
means = gpar.predict(x_test, num_samples=100)to get the predictive means, or
means, lowers, uppers = gpar.predict(
x_test,
num_samples=100,
credible_bounds=True
)to also get lower and upper 95% central marginal credible bounds. If you wish
to predict the underlying latent function instead of the observed values, set
latent=True in the call to GPARRegressor.predict.
Using keywords arguments, GPARRegressor can be configured to specify the
dependencies with respect to the inputs and between the outputs. The following
dependencies can be specified:
-
Linear input dependencies: Set
linear_input=Trueand specify the length scale withlinear_input_scale. -
Nonlinear input dependencies: This is enabled by default. The length scale can be specified using
scale. To tie these length scales across all layers, setscale_tie=True. -
Locally periodic input dependencies: Set
per=Trueand specify the period withper_period, the length scale withper_scale, and the length scale on which the periodicity changes withper_decay. -
Linear output dependencies: Set
linear=Trueand specify the length scale withlinear_scale. -
Nonlinear output dependencies: Set
nonlinear=Trueand specify the length scale withnonlinear_scale.
All nonlinear kernels are exponentiated quadratic kernels. If you wish to
instead use rational quadratic kernels, set rq=True.
All parameters can be set to a list of values to initialise the value for each layer separately.
To let every layer depend only the kth previous layers, set markov=k.
One may want to apply a transformation to the data before fitting the model,
e.g. transform_y keyword argument for GPARRegressor.
The following transformations are available:
-
log_transform:$y \mapsto \log(y)$ . -
squishing_transform:$y \mapsto \operatorname{sign}(y) \log(1 + |y|)$ .
Sampling from the model can be done with GPARRegressor.sample. The keyword
argument num_samples specifies the number of samples, and latent
specifies whether to sample from the underlying latent function or the
observed values. Sampling from the prior and posterior (model must be fit
first) can be done as follows:
sample = gpar.sample(x, p=2) # Sample two outputs from the prior.
sample = gpar.sample(x, posterior=True) # Sample from the posterior.The logpdf of data can be computed with GPARRegressor.logpdf. To compute the
logpdf under the posterior, set posterior=True. To sample missing data to
compute an unbiased estimate of the pdf, not logpdf, set
sample_missing=True.
Inducing points can be used to scale GPAR to large data sets. Simply set x_ind
to the locations of the inducing points in GPARRegressor.
import matplotlib.pyplot as plt
import numpy as np
from gpar.regression import GPARRegressor
from wbml.experiment import WorkingDirectory
import wbml.plot
if __name__ == "__main__":
wd = WorkingDirectory("_experiments", "synthetic", seed=1)
# Create toy data set.
n = 200
x = np.linspace(0, 1, n)
noise = 0.1
# Draw functions depending on each other in complicated ways.
f1 = -np.sin(10 * np.pi * (x + 1)) / (2 * x + 1) - x ** 4
f2 = np.cos(f1) ** 2 + np.sin(3 * x)
f3 = f2 * f1 ** 2 + 3 * x
f = np.stack((f1, f2, f3), axis=0).T
# Add noise and subsample.
y = f + noise * np.random.randn(n, 3)
x_obs, y_obs = x[::8], y[::8]
# Fit and predict GPAR.
model = GPARRegressor(
scale=0.1,
linear=True,
linear_scale=10.0,
nonlinear=True,
nonlinear_scale=0.1,
noise=0.1,
impute=True,
replace=False,
normalise_y=False,
)
model.fit(x_obs, y_obs)
means, lowers, uppers = model.predict(
x, num_samples=100, credible_bounds=True, latent=True
)
# Fit and predict independent GPs: set `markov=0` in GPAR.
igp = GPARRegressor(
scale=0.1,
linear=True,
linear_scale=10.0,
nonlinear=True,
nonlinear_scale=0.1,
noise=0.1,
markov=0,
normalise_y=False,
)
igp.fit(x_obs, y_obs)
igp_means, igp_lowers, igp_uppers = igp.predict(
x, num_samples=100, credible_bounds=True, latent=True
)
# Plot the result.
plt.figure(figsize=(15, 3))
for i in range(3):
plt.subplot(1, 3, i + 1)
# Plot observations.
plt.scatter(x_obs, y_obs[:, i], label="Observations", style="train")
plt.plot(x, f[:, i], label="Truth", style="test")
# Plot GPAR.
plt.plot(x, means[:, i], label="GPAR", style="pred")
plt.fill_between(x, lowers[:, i], uppers[:, i], style="pred")
# Plot independent GPs.
plt.plot(x, igp_means[:, i], label="IGP", style="pred2")
plt.fill_between(x, igp_lowers[:, i], igp_uppers[:, i], style="pred2")
plt.xlabel("$t$")
plt.ylabel(f"$y_{i + 1}$")
wbml.plot.tweak(legend=i == 2)
plt.tight_layout()
plt.savefig(wd.file("synthetic.pdf"))