A verifier for a simple imperative language powered by Z3
The grzb verifier implements both partial and total correctness rules of the standard Hoare logic. It can run in two modes: assuming that variables store either integers or reals. The generated proof obligations are discharged by Microsoft's Z3 SMT solver. Features include:
-
Recursive procedures with arguments passed by value or reference (example)
-
One-dimensional arrays (example)
-
Induction schemes for natural numbers (example)
The programs are written in LISP-y syntax:
In terminal:
$ cat examples/mult.imp
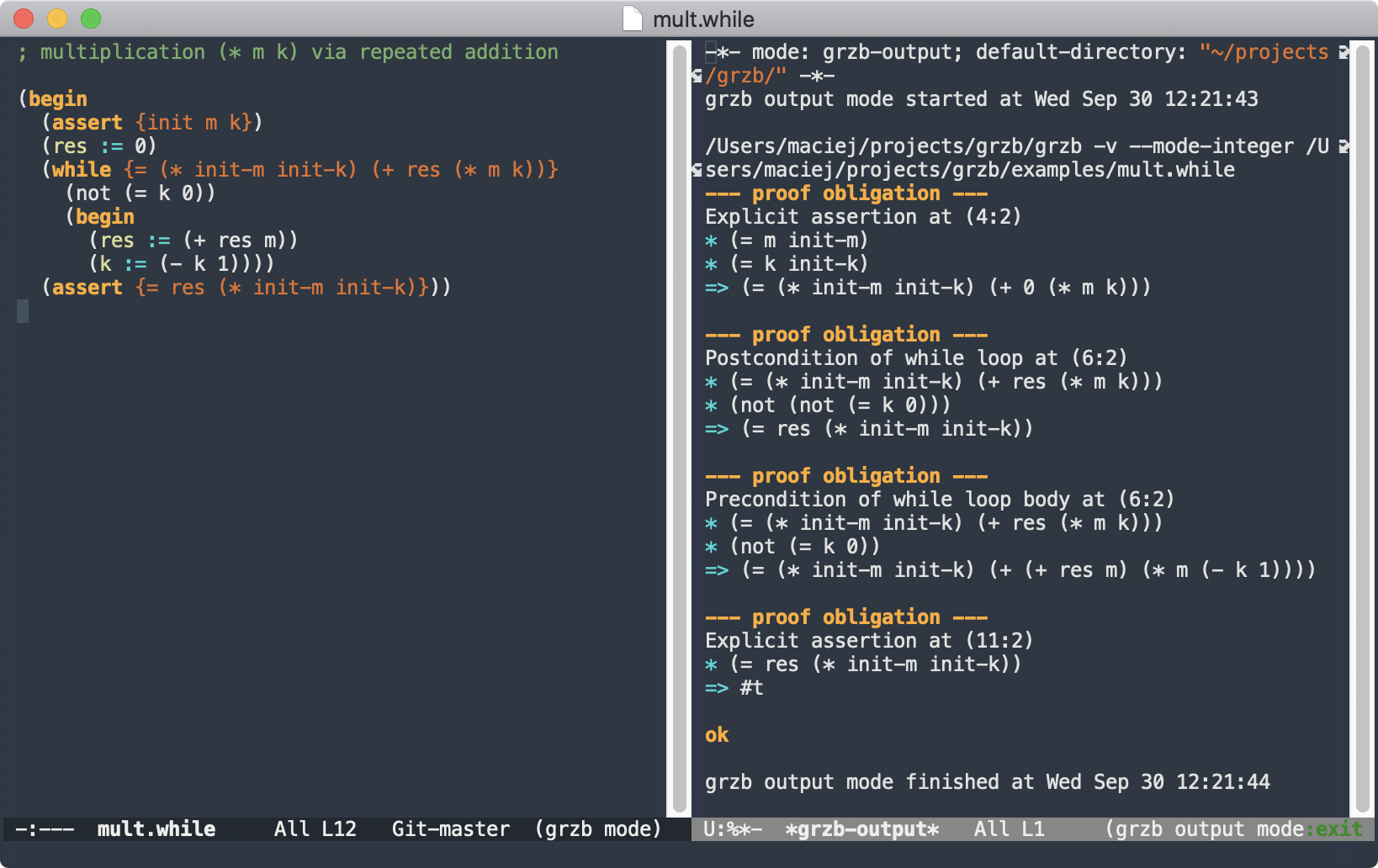
(begin
(assert {init m k})
(res := 0)
(while {= (* init-m init-k) (+ res (* m k))}
(not (= k 0))
(begin
(res := (+ res m))
(k := (- k 1))))
(assert {= res (* init-m init-k)}))
$ grzb examples/mult.imp
ok
grzb is available on Docker Hub. Just remember to bind the directory that contains the program you want to verify to the container's /home directory:
docker run --rm -t -v ~/projects/grzb/examples:/home maciejpirog/grzb:latest -v factorial.imp
Note that -v factorial.imp are the arguments given to grzb, where factorial.imp is a file stored in the ~/projects/grzb/examples directory.
ℹ️ You can also download and run the Docker grzb image from within Emacs. When in grzb-mode, simply hit C-c C-d C-c (or C-c C-d C-p for verbose output).
To compile grzb, you need Racket and Z3. For example, the following should do the trick on mac:
brew cask install racket
brew install z3
Then, make sure to set the Z3_LIB variable to point to Z3, e.g.,
export Z3_LIB=/usr/local/lib
As the next step, install the Racket bindings for Z3:
raco pkg install z3
Now we are ready to compile grzb:
cd grzb
raco exe -o grzb src/front/main.rkt
We can check if it works:
./grzb examples/factorial.imp
A-EXPR ::= (A-OP A-EXPR ...)
| n
| X
| (X . A-EXPR)
A-OP ::= + | - | * | / | %
where:
Semantics of the operators is as in Racket, where % is equivalent to Racket's mod.
n stands for a constant.
X standas for a variable (which could be any symbol).
(x . e) stands for the value of e-th cell of the array x.
Note that while arrays and variables share names, they are distinct. For example, in an expression (+ a (a . 2)) the first a is a variable (which stores a number), while (a . 2) is a value of the cell with index 2 of an array a, which has nothing to do with the a in the first argument of +.
B-EXPR ::= (B-OP B-EXPR ...)
| (B-CMP A-EXPR ...)
| true | false
B-OP ::= and | or | not | impl | iff
B-CMP ::= = | > | >= | < | <=
where:
not requires exactly one argumnet.
impl is an implication. In particular, (impl a b ... c z) is equivalent to (impl (and a b ... c) z).
PROG ::= (axiom LOG-EXPR) PROG
| (check LOG-EXPR) PROG
| (define (PROC-NAME X ...) LOG-EXPR LOG-EXPR CMD) PROG
| (define* (PROC-NAME X ...) LOG-EXPR LOG-EXPR A-EXPR CMD) PROG
| CMD
CMD ::= (skip)
| (begin CMD ...)
| (X := A-EXPR)
| ((X . A-EXPR) := A-EXPR)
| (if B-EXPR CMD CMD)
| (while LOG-EXPR B-EXPR CMD)
| (while* LOG-EXPR A-EXPR B-EXPR CMD)
| (PROC-NAME PROC-ARG ...)
| (assert LOG-EXPR)
| (dummy-po)
PROC-ARG ::= X
| (ref X)
| (val X)
| A-EXPR
(axiom f) tells grzb to include f as an assumption to every proof obligation. It is used to specify relations, as in the FACTORIAL example above. Free variables in every axiom are closed by a universal quantifier, so the following two definitions are equivalent:
(axiom {impl (> n 0) (FACTORIAL (- n 1) k) (FACTORIAL n (* k n))})
(axiom {forall (n k) (impl (> n 0) (FACTORIAL (- n 1) k) (FACTORIAL n (* k n)))})
Axioms are defined before the main statement of the program:
(axiom {FACTORIAL 0 1})
(axiom {impl (> n 0) (FACTORIAL (- n 1) k) (FACTORIAL n (* k n))})
(begin
(assert {>= n 0})
(res := 1)
(i := 0)
(while*
{and (FACTORIAL i res) (>= i 0) (<= i n)}
{- n i}
(< i n)
(begin
(i := (+ i 1))
(res := (* res i))))
(assert {FACTORIAL n res})))
(check f) run Z3 on a goal. As in the case of axioms, the formula f is always closed by a universal quantifier.
(define (foo x y z) pre post cmd) defines a recursive procedure named fooand arguments x, y, and z. The caller decides if the arguments are passed by value or reference. pre and post are pre- and postconditions of procedure call respectively. Procedures can be mutually recursive.
(define* (foo x y z) pre post v cmd) defines a total recursive procedure. The arithmetic expression v is the "variant", that is, a value which strictly decreases every recursive call. A group of mutually recursive procedures shares the variant.
(skip) is a command that does nothing.
(begin c d ...) is a sequential compositions of commands c, d, ...
(x := e) assigns the value of the arithmetic expression e to the variable x.
((x . e) := f) assigns the value of the arithmetic expression f to the e-th cell of the array a.
(if b c d) is the obvious "if" command.
(while i b c) is the while loop, where i is the invariant. It yields partial correctness of the loop.
(while* i v b c) is the while loop that yields total correctness. The arithmetic expression v is the "variant" of the loop, that is, a value which strictly decreases every iteration.
(foo x y z) invokes the procedure foo with arguments x, y, z. An argument could be:
-
a variable, in which case it is passed by reference,
-
(ref x)for a variablex, which also means passingxby reference, -
(val x)for a variablex, which means passingxby value -
an arithmetic expression, which is (of course) passed by value (except for the case when the arithmetic expression is a single variable).
(assert f) is a user asserion which specifies a condition that is met at a given point of the program. Most usually, we want one as the first step of the program (the precondition) and the last step (the postcondition).
(dummy-po) adds a trivial proof obligation with the current weakest precondition as an assumption. This is useful to reveal the computed precondition.
LOG-EXPR ::= (B-OP LOG-EXPR ...)
| (B-CMP A-EXPR ...)
| true | false
| (forall (X ...) LOG-EXPR)
| (exists (X ...) LOG-EXPR)
| (REL A-EXPR ...)
| (init X ...)
| (INDUCTION-SCHEME (X) LOG-EXPR)
where:
(X ...) stands for a non-empty list of variables (symbols)
REL is a name of a relation. Relations are user-specified (via axiom statements), e.g., one can specify (in the style of logic programming) a relation FACTORIAL such that (FACTORIAL n k) holds if k is a factorial of n:
(axiom {FACTORIAL 0 1})
(axiom {impl (> n 0) (FACTORIAL (- n 1) k) (FACTORIAL n (* k n))})
As a convention, we write verification logic expressions in curly braces (except of course the constants true and false) and we use all-caps for names of relations.
Note that arrays are not first-class in the program, they can be referenced as arguments to relations (by adding a quote, e.g. 'a), and bound by special quantifiers forall-array and exists-array. For example, a predicate that states that the part of an array in the bounds [i .. j] is sorted can be defined as the following relation:
(axiom {impl (<= i j) (iff (SORTED 'a i j)
(forall (k m) (impl (<= i k m j)
(<= (a . k) (a . m)))))})
Since free variables in axioms are closed by universal quantifiers, the above is synonymous to:
(axiom (forall-array (a) (forall (j i)
(impl (<= i j) (iff (SORTED 'a i j)
(forall (k m) (impl (<= i k m j)
(<= (a . k) (a . m))))))))
(init x y ... z) is a macro for (and (= x init-x) (= y init-y) ... (= z init-z)). It is useful as the initial assertion.
(INDUCTION-SCHEME (x) f) is a macro for induction on natural numbers, where f stands for a predicate with a free variable x. Because nothing in grzb is higher-order, we need to generate a new induction theorem for every predicate separately. There are two predefined recursion schemes:
(induction (x) (P x)) stands for:
(impl (P 0)
(forall (x) (impl (>= x 0) (P x) (P (+ x 1))))
(forall (x) (impl (>= x 0) (P x))))
while
(induction< (x) (P x)) stands for
(impl (forall (x) (impl (>= x 0)
(forall (y) (impl (>= y 0) (< y x)
(P y)))
(P x)))
(forall (x) (impl (>= x 0) (P x))))
For example, Z3 is not able to accept the following program without the induction axiom:
(axiom {EVEN 0})
(axiom {impl (>= n 0) (EVEN n) (EVEN (+ n 2))})
(axiom {induction (x) (or (EVEN x) (EVEN (+ x 1)))})
(begin
(assert {>= x 0})
(y := (+ x 1))
(assert {or (EVEN x) (EVEN y)}))
❗ Induction axioms are (of course) not sound in the real mode.