A couple of years ago I had to come up with a project for a course and decided to code a Neural Network in C++.
This repository is a slightly brushed up version of this project, it makes use of the original Neural Network class written for the course (header/NeuralNetwork.h) and I have added python scripts for conveniently generating data and plotting errors.
The pipeline
- creates training and testing samples of the XOR or CSWAP gate (a 3-bit gate)
- fits the model to the training data and evaluates the performance on the test set.
- creates a plot of the error measure
Logical Gates | Neural Network | Pipeline
The Neural Network (header/NeuralNetwork.h) can be initialized with different numbers of neurons in each layer. This invites to experiment with more exotic types of gates - but first:
Logical gates such as e.g. AND, OR can typically modeled by a single perceptron. The exclusive OR (XOR) is an exception to that as it is not linearly separable and a Neural Network requires a hidden layer to emulate it.
The XOR returns True if the inputs are distinct and False otherwise:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The Controlled SWAP (CSWAP) gate or Fredkin gate (wikipedia) has 3 input and 3 output bits and can be used in Quantum Computing. It works as follows:
If the C-bit is non-zero, Input 1 and Input 2 are switched. This is conveyed in the following table
| C | Input 1 | Input 2 | C | Output 1 | Output 2 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
The Neural Network has 3 layers: input, output and a hidden layer*. The numbers of neurons per layer is variable and the number of input/output neurons will be inferred from the data provided.
For the XOR gate, the network will have 2 inputs and 1 output. In the case of the CSWAP gate the network will have 3 inputs and 3 outputs. The number of hidden neurons is 2 by default and should be adjusted upwards when training the model on CSWAP data.
As activation function the hyperbolic tangent function is used: tanh(x)
Loss: Root Mean Square error (RMS):
where the index i runs over all neurons of the layer (here that is only one).
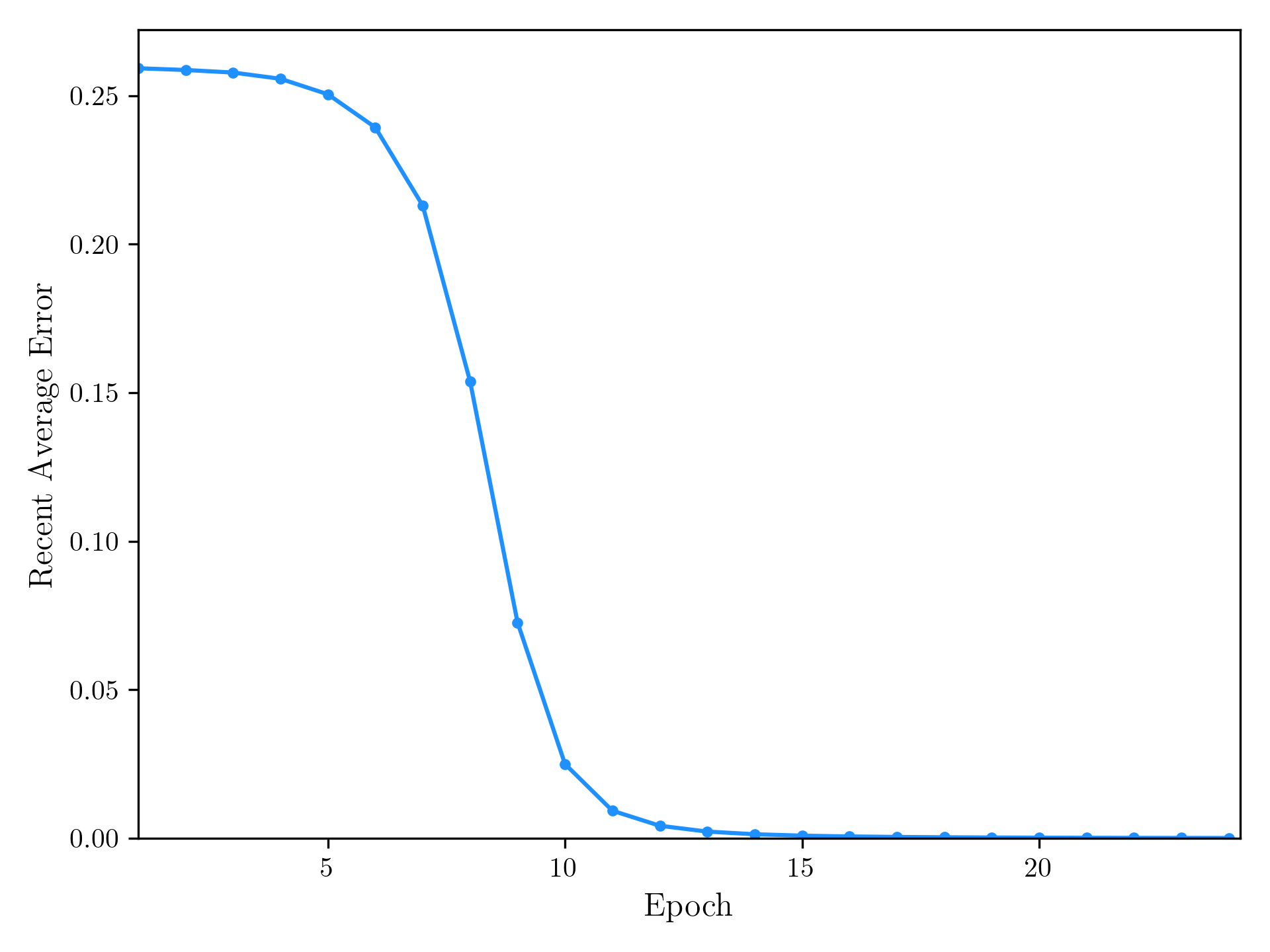
At every step a smoothed error measurement (RAE) is put out, recursively it can be defined like this:
with the smoothing factor xi. The intuition here is: the smoothing factor adjusts how much a single loss value contributes to the RAE
By default the training goes over 30 epochs but the loop is broken as soon as the RAE drops below a certain threshold (0.0001).
g++ -o data_gen data_gen_XOR.cpp
./data_genor
g++ -o data_gen data_gen_CSWAP.cpp
./data_genby default this creates 250 training samples and 100 test samples.
g++ -o training training.cpp
./trainingThe default settings are
- learning rate (eta) = 0.08
- momentum (alpha) = 0.1
Note: When training on the CSWAP data, the Neural Network will automatically initialized with 3 Input and 3 Output neurons, however 2 hidden neurons appear to be insufficient to train the network!
The plotting script utilizes numpy and matplotlib:
pip install numpy
pip install matplotlibthen run
python plot.py to obtain a plot like this: