Date written: December 2020
This project was pursued as my final project for MECH 579 (Multidisciplinary Design Optimization, i.e. MDO) at McGill University, taught by Professor Nadarajah of the Mechanical Engineering department.
In the field of computational fluid dynamics (CFD), the discontinuous Galerkin (DG) method is a widely used high-order numerical method for discretizing partial differential equations (PDEs). In the DG method, the computational domain is discretized into elements, this is referred to as the mesh, and within each element, the solution is locally reconstructed by polynomials of order P. Favourably, the method allows for discontinuities between elements by employing a numerical flux (i.e. an approximate Riemann solver). For a problem in which high-gradient regions are present, a mesh that conforms to these high-gradient locations would reduced the error between the numerical and exact solution, while keeping the number of elements and P constant. It is such a mesh that is the motivation of this project, to use an optimization algorithm to determine the optimal location of the element vertices such that the DG solution error is minimized.
In this project, the equation to be solved using DG is the steady-state linear advection equation, in which a manufactured high-gradient solution is chosen. An unconstrained optimization algorithm, the Quasi-Newton line-search algorithm, is employed to minimize the error of the DG solution, computing the gradient numerically using the finite-difference method, while the hessian is computed numerically using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method. For more details, refer to the report by clicking here.
From the results above we see that the initial L2-error has been successfully decreased by 2 orders of magnitude by optimizing the vertex locations. From the optimization path of vertices with the exact solution superimposed, we see that the vertices move towards the closest high-gradient region, as expected.
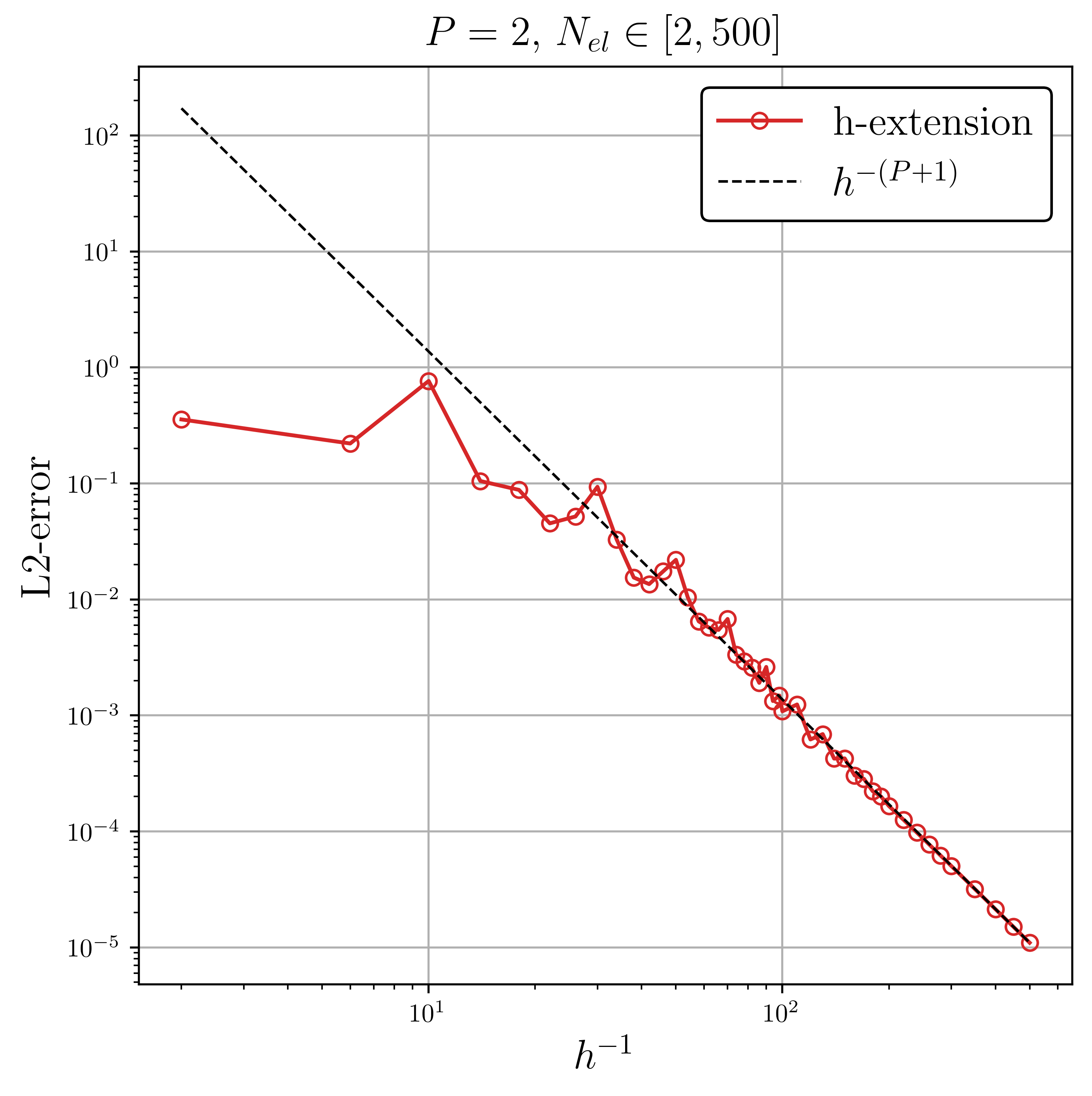
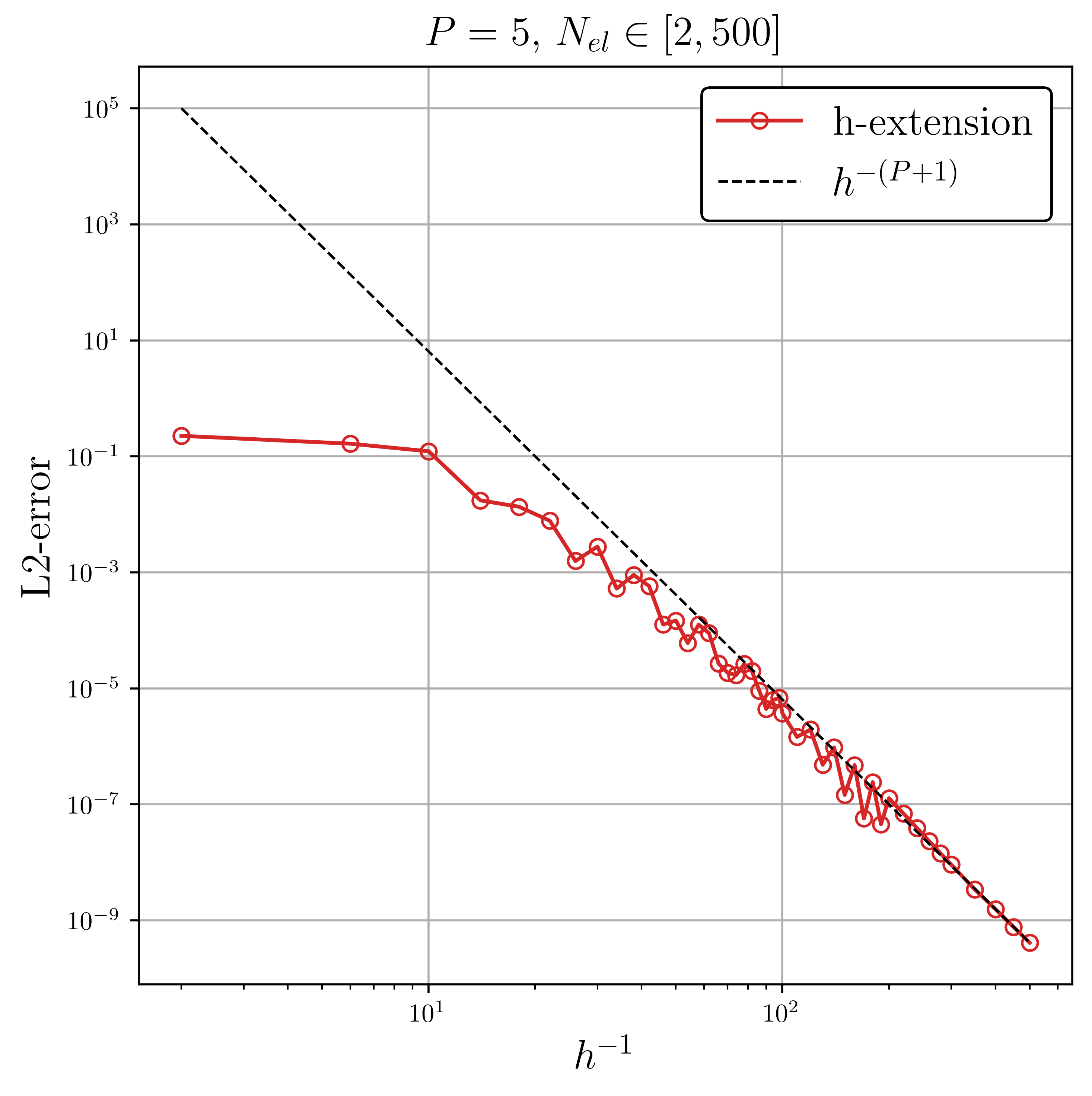
The DG solver parameters were selected such that the DG solution is sufficiently smooth to apply finite- difference for computing the gradient of the objective function, while having an initial L2-error that does not lie on the spectral convergence asymptote. In addition, the need for an initial sufficiently smooth DG solution was needed to avoid having vertex overlap as an unconstrained optimization algorithm was used and cannot guarantee this will never occur.
On the other hand, the optimization parameters were selected such that the algorithm performed acceptably; these were determined by trial and error.