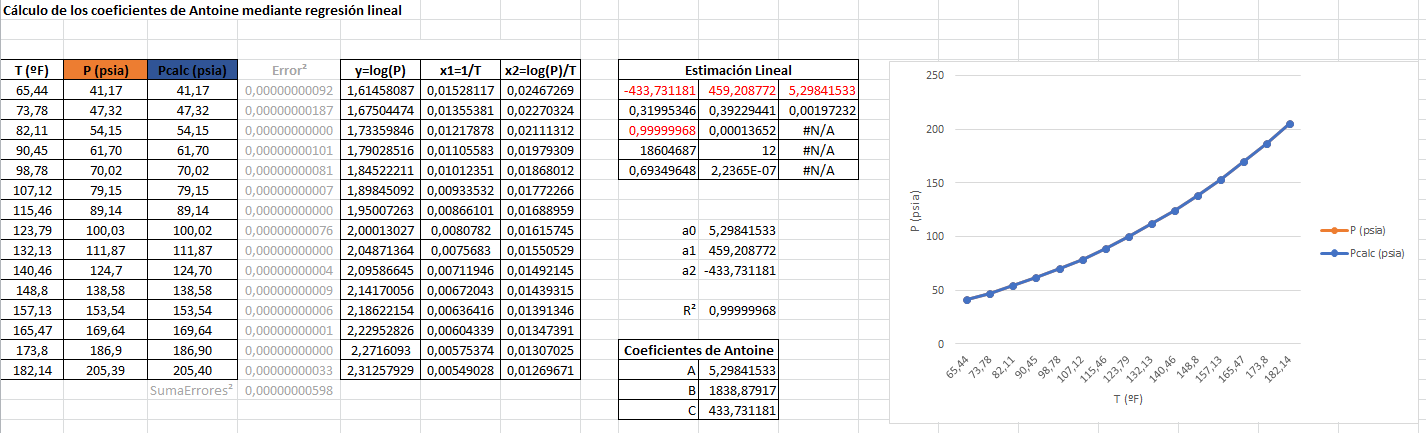
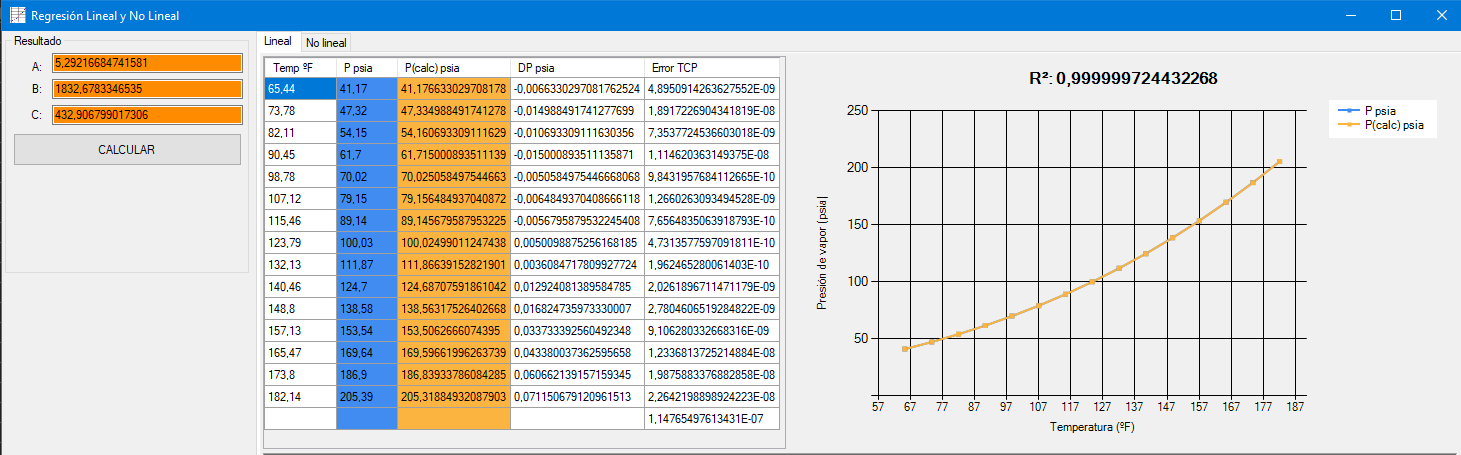
log(P)=A−B/(T+C)
Para ello utilizaremos Excel como herramienta básica que casi todos conoceréis y tendréis instalada en vuestro equipo y además veremos como afrontar este tipo de problemas en .NET con la ayuda de una librería externa bastante interesante como es Accord. No es la intención de esta entrada profundizar en conceptos matemáticos complejos ni entrar en detalle en el concepto de regresión, más bien se pretende dar unas pinceladas para poder ser capaces de plantear y resolver problemas similares.
| Temperatura (ºF) | Presión (psia) |
|---|---|
| 65,44 | 41,17 |
| 73,78 | 47,32 |
| 82,11 | 54,15 |
| 90,45 | 61,70 |
| 98,78 | 70,02 |
| 107,12 | 79,15 |
| 115,46 | 89,14 |
| 123,79 | 100,03 |
| 132,13 | 111,87 |
| 140,46 | 124,70 |
| 148,80 | 138,58 |
| 157,13 | 153,54 |
| 165,47 | 169,64 |
| 173,80 | 186,90 |
| 182,14 | 205,39 |
https://www.youtube.com/watch?v=t-vXfZ1xUvU
| Excel lineal | Excel no lineal (GRG) | .NET lineal | .NET no lineal (LM) | |
|---|---|---|---|---|
| A | 5,2984 | 4,8213 | 5,2921 | 4,9822 |
| B | 1838,8791 | 1348,0797 | 1832,6783 | 1497,0177 |
| C | 433,7311 | 354,4275 | 432,9067 | 378,3875 |
| SumaErrores² | 5,98×10-9 | 6,44×10-5 | 1,14×10-7 | 5,39×10-5 |
| R² | 0,99999968 | – | 0,99999972 | – |
La parte de la regresión lineal no tiene mayor complicación y tanto en Excel como en NET son fáciles y rápidos de implementar.
La parte de regresión no lineal no es que sea muy compleja ya que tanto Excel como Accord nos lo ponen bastante fácil, pero si es cierto que requiere que pongamos algo más de nuestra parte para obtener buenos resultados. Los algoritmos de optimización no lineal usados no han sido los mismos, Solver de Excel utiliza el algoritmo GRG (Gradiente Reducido Generalizado) y Accord dispone de los algoritmos Gauss-Newton y Levenberg-Marquardt, siendo éste último el implementado. Estos algoritmos son similares y ambos nos devuelven un mínimo local, es decir, no te dan la mejor solución pero sí una muy próxima. Estos algoritmos necesitan que les indiquemos unos valores iniciales de los parámetros o coeficientes que va a alterar para buscar una solución, y la solución obtenida depende de esos valores iniciales, por lo que tanto en Excel como en NET se ha partido de los valores 2, 1500, 273 para A, B y C respectivamente.
En general Excel es una gran herramienta que facilita el trabajo enormemente y de la que podemos sacar chispas en nuestro día a día, pero me apetecía darle una vuelta a la posibilidad de resolver problemas de optimización con un lenguaje de programación y palpar cuan fácil es obtener «eso» que con Excel se obtiene tan rápido. Espero que os sirvan los ejemplos y que los disfrutéis tanto como yo.
Más información en la entrada del blog: https://garikoitz.info/blog/2021/06/regresion-lineal-y-no-lineal-excel-vs-net/