CANOPUS - Parameter Estimation for Large-Scale Channel Models

Wireless Telecommunications
My Linkedin

Description

In wireless telecommunications, the signal strength decreases or attenuates during transmission, especially over long distances. The attenuation increases exponentially with the distance between the transmitter and the receiver. This report attempts to assist in estimating the attenuation in different conditions. One common model for path loss estimation is the Path Loss Exponent and Shadowing Gaussian Noise models in urban environments, which we will explore using machine learning techniques.

Tools

• Python
• sklearn
• pandas
• numpy
• matplotlib
• IPhone 8
• Network Cell Info Lite

Problem

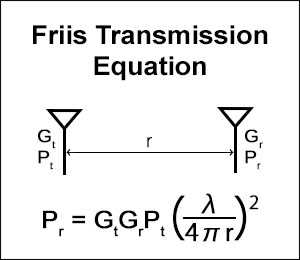
In telecommunications engineering, the Friis equation, also known as the free space path loss (FSPL) equation, is used to calculate the power received by an antenna at a certain distance from a transmitting antenna. The equation depends on factors like transmitted power (Pt), transmitting antenna gain (Gt), receiving antenna gain (Gr), and distance (d).

To calculate the path loss (PL) and power received (Pr), we can simplify the Friis equation as follows:

$$Pr = P_{t} \cdot G_{t} \cdot G_{r} \left( \frac{\lambda}{4 \pi R} \right)^2$$

or in logarithmic form:

$$Pr = P_{t} + G_{t} + G_{r} - P_{L}$$

where the path loss is:

$$P_{L}= \beta \cdot 10~log_{10}(\frac{4\pi d}{\lambda})$$

Further simplifying, we get:

$$P_{r}= P_{0} - \beta \cdot 10~log_{10}(\frac{d}{d_{0}}) + X_{\sigma}$$

Here, $X_{\sigma}$ is Gaussian noise with zero mean and variance $\sigma^2$.

Parameter	Description
$P_{0}$	the reference received power
$d_{0}$	reference distance
$X_{\sigma}$	Gaussian noise with standard deviation between 4 and 12

The goal of this project is to estimate the parameters $\beta$ and $X_{\sigma}$ through data collection and regression.

Execution

1.Data Collection

We collected data by measuring signal quality between a mobile phone and three base stations, including both line-of-sight (e.g., streets) and non-line-of-sight locations (e.g., parks). Sampling was done every second during movement, with 81 data samples collected. Figure 1 shows a map of the sample points and base stations, indicating locations where signal quality deteriorated due to obstructions such as buildings and narrow streets. The data was gathered from 3 separate base stations.

Figure 1: Route map and sampling of base stations along with color display of signal quality

2.Reference Value Estimation

By applying regression techniques to the collected data, we estimated the reference received power $P_{0}$​ and the reference distance $d_{0}$. In this experiment, a reference distance of 10 meters was assumed, and we calculated $P_{0}$​ to be approximately -64 dBm, as shown in Figure 2.

Figure 2: changes in Signal Quality in relation to Distance from the base station

3.Path Loss Coefficient and Noise Estimation:

By fitting a curve to the signal strength data, we estimate the path loss coefficient

$$\beta : 1.5035$$

and the noise standard deviation

$$\sigma : 13.4487$$

Data & Script

The gathered data and python scripts are all provided here

Reference

E. D. O. Shoewu, L. Akinyemi, J. Emagbetere, and F. Edeko, "Path loss in Nigerian rural vegetation area: A case study in Igbaraoke, Ondo state," November 2014.