MATDES: A Comprehensive MATLAB Implementation of the Data Encryption Standard (DES)

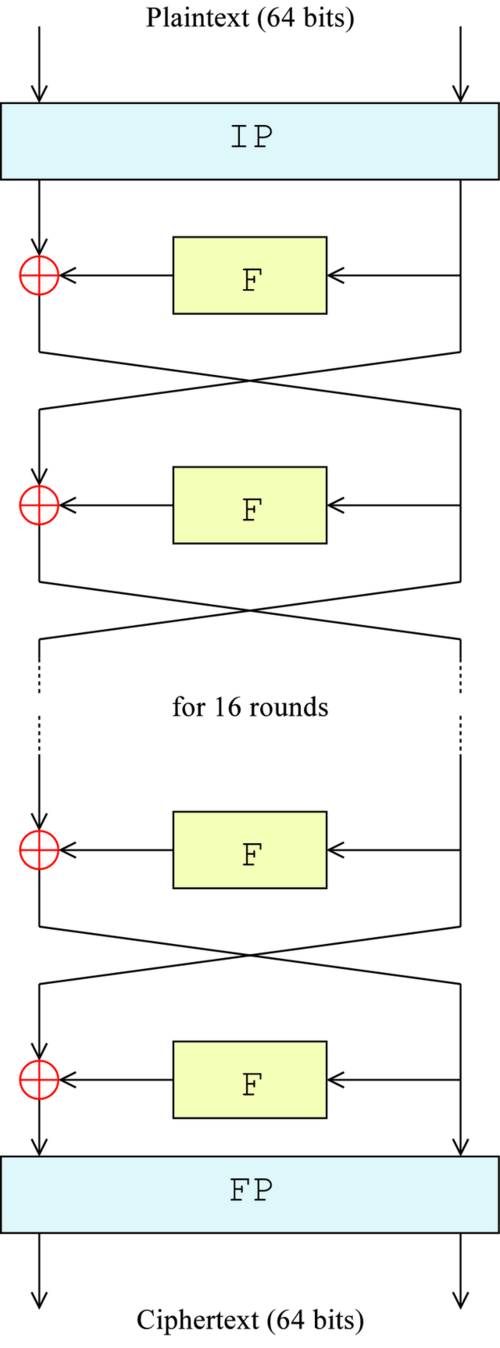
The Data Encryption Standard (DES) is a symmetric-key encryption algorithm that has been a cornerstone of electronic data security since its standardization in 1977. It relies on a 64-bit block cipher with a 56-bit key.

DES operates through 16 rounds of complex transformations, which include permutation and substitution methods. These multiple rounds add to the complexity and strength of the encryption. The process consists of the following primary components:

1. Initial Permutation $IP$: The data block is initially reordered.
2. Round Function: The core encryption process, repeated 16 times, involving key mixing, substitution, and permutation.
3. Final Permutation $IP^{-1}$: The reverse of the initial permutation.

Below is a high-level overview of the DES process:

This document presents a MATLAB implementation of DES, detailing the design, functionality, and overall structure of the algorithm.

Sub-key Function: Key Generation for Each Round

An essential aspect of the DES algorithm is the sub-key generation function. This function takes a 56-bit string, K_pc_1 (derived from the main key), and an index, then creates each sub-key K_i for a specific round of encryption or decryption. The argument "operation" is also accepted by this function, determining whether it should perform key generation for encryption or decryption.

The sub-key is given by:

$$ K_i = PC_2(C_0 << n || D_0 << n) $$

where PC_2 is a permutation that maps a 56-bit string to a 48-bit string, << n is a left bitwise rotation, and n is defined by:

$$ n = \begin{cases} 1, & \text{if } i = 1, 2, 9, 16 \\ 2, & \text{else} \end{cases} $$

where i belongs to the set {1, ..., 16}. This is achieved in MATLAB using a for-loop to shift each half.

Counting Unique Keys: Ensuring Key Diversity

The diversity of the keys used in the DES algorithm can be calculated by assessing the number of unique sub-keys derived from the main key, K. To do this, we populate an array with all 16 sub-keys, and then use the built-in MATLAB function unique(), which returns an array of unique sub-keys when passed our array.

Round Function: Encrypting in Stages

The round function is the workhorse of each encryption cycle. This function accepts a 64-bit block, divided into a left half and right half, and a 48-bit sub-key, K_i. It performs a series of operations to transform the input block.

The f-function: A Three-Step Transformation

The f-function is a composite function that performs three primary operations: expansion, S-box substitution, and permutation. These steps contribute to the overall security of the DES encryption process.

Expansion

The expansion function E maps 32 bits to 48 bits. The expansion table is defined in MATLAB as an array and uses the logic given by Algorithm 1. This component provides diffusion.

S-box Substitution

The S-box substitution is one of the main components that gives DES its security, as it provides confusion. The output of each S-box is determined by the 6-bit "selection bits" where the row is given by bits 1 and 6, and the column is given by bits 2-5. The row and columns are then converted to decimal using the bin2dec() function. In reality, the row and columns are incremented by 1 to account for MATLAB's matrix indexing convention.

Permutation

This permutation uses Algorithm 1 and maps a 32-bit string to a 32-bit string.

Implementing the DES Algorithm

Now, using the sub-key generation function and the round function, we can implement the DES algorithm. The only remaining steps are to apply the initial permutation IP, the initial key permutation PC_1, and the final permutation IP^-1.

The logic for DES is given by:

Algorithm DES (plainText, key, operation)
plainText <- hexToBin(plainText)
key <- PC_1(key)
[leftHalf, rightHalf] <- IP(plainText)
for i <- 1 to 16 do
  [leftHalf, rightHalf] <- round(leftHalf, rightHalf, K_i)
end
cipher <- rightHalf || leftHalf
cipher <- IP^-1(cipher)
cipher <- binToHex(cipher)

Decryption: Reverse Engineering the Encrypted Text

One of the significant advantages of DES is that encryption and decryption are mirror processes. The decryption algorithm uses the same functions as mentioned above. However, instead of plaintext, the input is now the encrypted text. Thus, DES provides a symmetric encryption and decryption process.

The decryption operation redefines the sub-key generation as:

$$ K_i = PC_2(C_0 >> n || D_0 >> n) $$

where PC_2 stays the same, >> n is a right bitwise rotation, and n is defined by the same conditions as for encryption. This essentially reverses the order of the key generation, i.e., (K_16, ..., K_1).