A virtual Rubik's Cube implemented using the Kociemba algorithm for solving scrambled states. This project offers an interactive 3D simulation of a Rubik's Cube that you can scramble, manipulate manually, and solve. The solution is computed using the Kociemba two-phase algorithm, widely known for its efficiency in solving Rubik's cubes with minimal moves.
Deployment: This project is deployed using a WebGL server with Node.js alongside GitHub Pages for hosting the live demo.
Heavily Inspired by: @Megalomobile
Click here for the Live Demo | Vercel
- Interactive 3D Cube: Manipulate the cube by dragging and rotating different layers in 3D space.
- Scramble & Solve: Automatically scramble the cube or solve any configuration using the Kociemba algorithm.
- Unity/Blender Simulation: Visual simulations and demos showcasing the solution steps.
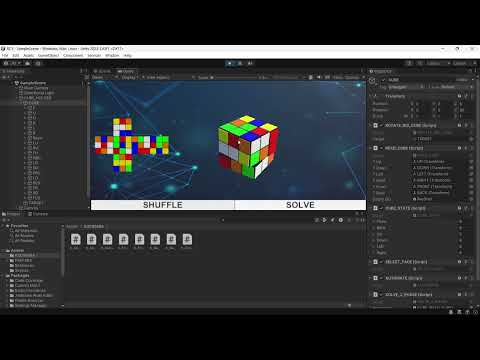 |
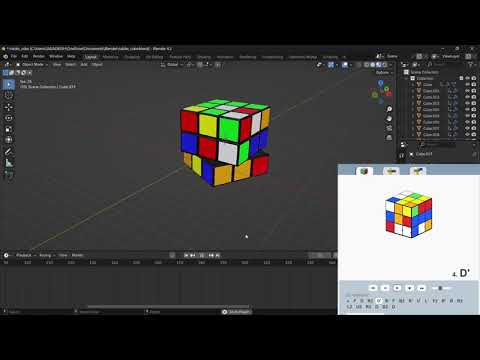 |
|---|---|
| Unity 3D Simulation | Blender Simulation |
This project leverages the pre-existing Kociemba two-phase algorithm for Rubik's Cube solving, and our main contribution has been the seamless integration of this algorithm into a Unity-based simulation. The role of the solver is crucial, as it computes the solution when a scrambled cube is presented.
We designed the system to fetch cube states directly from the user interface, where users can scramble or manipulate the cube. Upon clicking the "Solve" button, the Kociemba algorithm works under the hood to generate an optimal solution, which is then passed to the Unity engine. The Unity environment simulates this solution visually, step by step, allowing users to see the cube's transformation in real-time.
The Blender solution demo featured here is purely a visual mockup, simulating how the cube might appear when following a solved sequence. It serves as a demonstration for visual feedback but has no direct involvement in the solving process or algorithm implementation. This is an intermediate step showcasing the solution process and will be further integrated into Unity for enhanced user interaction.
- Right Click + Drag: Rotate the entire cube in 3D space.
- Left Click + Drag on Layers: Rotate specific layers of the Rubik's Cube.
- SCRAMBLE: Randomly scrambles the Rubik's Cube.
- SOLVE: Solves the scrambled cube using the Kociemba solver. (Note: Initial solve may take some time to compute.)
To run the project locally, follow these steps:
-
Clone the repository:
git clone https://github.com/Mummanajagadeesh/v-rubiks-cube.git cd v-rubiks-cube -
Open the project in your preferred IDE or deploy it on a web hosting service.
-
To modify or extend the project, ensure you have:
- A working knowledge of 3D engines such as Unity or Blender.
- Familiarity with the Kociemba algorithm and basic Rubik’s Cube concepts.
This project uses the Kociemba two-phase algorithm, which is an optimized approach for solving the Rubik's Cube in under 20 moves. The first phase reduces the problem to a manageable subset of configurations, and the second phase finds an optimal solution from that subset.
- The first time you run the solver, it may take longer due to the initial calculation of move tables.
- Subsequent solves will be faster as the tables are cached.
We have exciting plans for the future of this project:
- Hardware Integration: The next step is to bring this solution into the physical world. Using computer vision (CV) techniques, we aim to read the Rubik's Cube faces via a camera and translate the detected state into a solvable format.
- 3D Design: We are currently working on the 3D design of the hardware, which is under construction. This will involve a mechanism where gripper-like structures hold and manipulate the cube for solving.
- Optimization: Another goal is to reduce the time required for solving, making the process as fast and efficient as possible.
- Physical Cube Solving: Ultimately, the project will be able to solve a real Rubik's Cube using robotic structures that simulate the virtual environment.
We are open to contributions from anyone interested in participating in this exciting journey. If you'd like to help us push the project forward, feel free to reach out!
This project is licensed under the MIT License.
Enjoy solving the cube! 🎲