README.Rmd

---
output: github_document
---

<!-- README.md is generated from README.Rmd. Please edit that file -->

```{r, include = FALSE}
knitr::opts_chunk$set(
  collapse = TRUE,
  comment = "#>",
  fig.path = "man/figures/README-",
  out.width = "100%"
)
```

# fort &#x2656; fast orthogonal random transforms

<!-- badges: start -->

[![](https://img.shields.io/badge/package-fort-blue?logo=r)](https://github.com/tomessilva/fort)

<!-- badges: end -->

The `fort` package provides convenient access to fast, structured, random linear transforms implemented in C++ (via 'Rcpp') that are (at least approximately) orthogonal or semi-orthogonal, and are often much faster than matrix multiplication, in the same spirit as the [Fastfood](#ref4), [ACDC](#ref3), [HD](#ref2) and [SD](#ref1) families of random structured transforms.

Useful for algorithms that require or benefit from uncorrelated random projections, such as fast dimensionality reduction (e.g., [Johnson-Lindenstrauss transform](#links)) or kernel approximation (e.g., [random kitchen sinks](#ref5)) methods.

For more technical details, see the reference page for [`fort()`](https://tomessilva.github.io/fort/reference/fort.html).

## Illustration

This plot shows a speed comparison between using a fort-type transform *vs.* a matrix multiplication, for different transform sizes, on commodity hardware.

![](https://tomessilva.github.io/img/fort_speed.png)

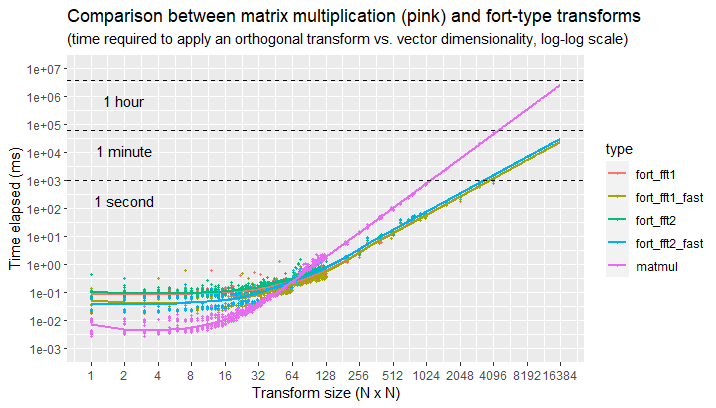
Here we can see that, for transform sizes in spaces larger than $\mathbb{R}^{64}$, you can obtain significant speed-ups through the use of structured transforms (such as the ones implemented in `fort`) instead of matrix multiplication. In particular, the time elapsed can go down by 10 to 100 times, for practical transform sizes (e.g., an orthogonal transform in $\mathbb{R}^{4096}$ can take a second, instead of a minute).

## Installation

You can install the development version of `fort` from [GitHub](https://github.com/) with:

``` r
# install.packages("devtools")
devtools::install_github("tomessilva/fort")
```

Note: you will need to have the `Rcpp` and `RcppArmadillo` packages
installed, as well as a working
[build environment](https://cran.r-project.org/bin/windows/Rtools/)
(to compile the C++ code), in order to install a development version
of `fort`.

## Example

This is a basic example which shows how to use `fort` in practice:

```{r example}
library(fort)

(fast_transform <- fort(4)) # fast orthogonal transform from R^4 to R^4

matrix_to_transform <- diag(4) # 4 x 4 identity matrix
(new_matrix <- fast_transform %*% matrix_to_transform) # transformed matrix

(inverse_transform <- solve(fast_transform)) # get inverse transform

round(inverse_transform %*% new_matrix, 12) # should recover the identity matrix
```

Here is a comparison of using a `fort` transform against a simple matrix multiplication, in terms of speed:

``` r 
library(fort)

matrix_to_transform <- diag(1024) # 1024 x 1024 identity matrix

fast_transform <- fort(1024) # fast orthogonal transform from R^1024 to R^1024
slow_transform <- as.matrix(fast_transform) # the same, but in matrix form

# time it takes for the fast transform
system.time(for (i in 1:100) test <- fast_transform %*% matrix_to_transform, gcFirst = TRUE)
#>   user  system elapsed 
#>   5.50    2.12    8.00

# time it takes for the equivalent slow transform (via matrix multiplication)
system.time(for (i in 1:100) test <- slow_transform %*% matrix_to_transform, gcFirst = TRUE)
#>   user  system elapsed 
#>  70.57    0.61   77.95 
```

Note: in this case, using a `fort` fast transform leads to a speed-up of
about 10x compared to the use of matrix multiplication.

For more information on how to use `fort` in practice, check out the [package's vignette](https://tomessilva.github.io/fort/articles/fort-basic.html).

## License

MIT

## [Useful links]{#links}

 - [fort 0.01 package manual (pdf)](https://tomessilva.github.io/manuals/fort_0.0.1.pdf)

 - [Random projection (Wikipedia)](https://en.wikipedia.org/wiki/Random_projection)

 - [Johnson-Lindenstrauss lemma (Wikipedia)](https://en.wikipedia.org/wiki/Johnson%E2%80%93Lindenstrauss_lemma)

## References

 1) [Krzysztof M. Choromanski, Mark Rowland, and Adrian Weller. "[The unreasonable effectiveness of structured random orthogonal embeddings.](https://web.archive.org/web/20230210084852/https://proceedings.neurips.cc/paper/2017/file/bf8229696f7a3bb4700cfddef19fa23f-Paper.pdf)", NIPS (2017).]{#ref1}

 2) [Felix Xinnan X. Yu, Ananda Theertha Suresh, Krzysztof M. Choromanski, Daniel N. Holtmann-Rice, and Sanjiv Kumar. "[Orthogonal random features.](https://web.archive.org/web/20230730083009/https://proceedings.neurips.cc/paper_files/paper/2016/file/53adaf494dc89ef7196d73636eb2451b-Paper.pdf)", NIPS (2016).]{#ref2}
 
 3) [Marcin Moczulski, Misha Denil, Jeremy Appleyard, and Nando de Freitas. "[ACDC: A structured efficient linear layer.](https://web.archive.org/web/20221206143544/https://arxiv.org/pdf/1511.05946.pdf)", arXiv:1511.05946 (2015).]{#ref3}

 4) [Quoc Le, Tam&#225;s Sarl&#243;s and Alex Smola. "[Fastfood - approximating kernel expansions in loglinear time.](https://web.archive.org/web/20230518190102/https://proceedings.mlr.press/v28/le13-supp.pdf)", ICML (2013).]{#ref4}

 5) [Ali Rahimi, and Benjamin Recht. "[Random features for large-scale kernel machines](http://web.archive.org/web/20230316191621/https://proceedings.neurips.cc/paper/2007/file/013a006f03dbc5392effeb8f18fda755-Paper.pdf)", NIPS (2007).]{#ref5}