ADE-Python is the finite volume method based Advection-Diffusion Equation Solver. Which can be very useful to simulate various transport phenomenon like flow of concentration, temperature, enerygy or momemtum in a media.
The Python scipts are writted in very basic programming language, any newcomer can easily understand our code and contribute further.
We've implemented first order time implicit scheme because of its unconditionally stability, so you can use any length of time scale.
To evaluate the value of fluxes at the interefernce of Control Volume, it uses power-scheme used by Suhas Patankar(1980). But you can use other below mentioned by chosing the A(P) fuction in the discretisation script
This project have been processed into two part i.e 2D unstructured grid and 3D structured grid.
This part can only handly cuboidal geometery with cuboidal mesh elements. Simple numpy 3D array is used to create mesh of the geometry. We've used Line-by-Line solver which is an iterative solver, which is much slower than direct solvers but always give you realistic solution for any input conditions.
You can create any complex 2D geometry using the Pygmsh. Triangular Mesh elements are used and seperate class module is made to handle Mesh Topography information which increases complexity. Direct Solver numpy.linalg.solve is used to solve the linear equations for this part.
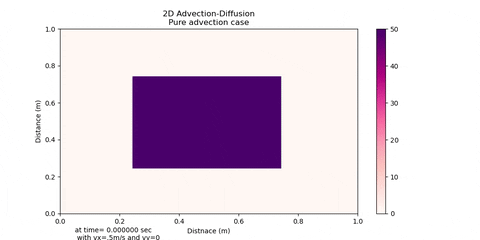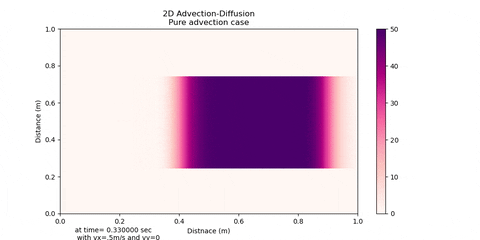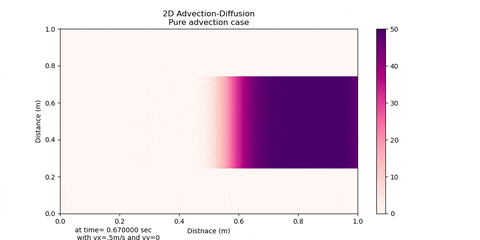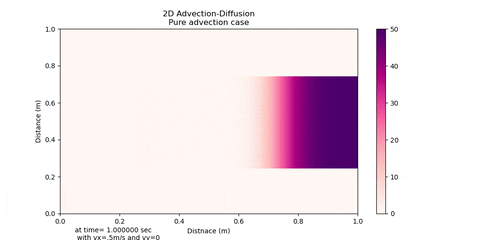
This solver gives significant False Diffusion for Peclet No greater than 10 due to upwind scheme of advection that'd been implemented. Although you can decrease this false diffusion by using very fine meshing and compromising computational time
You can see the False Diffusion in advection direction. But don't worry this solver works good for simulations when your Peclet No. is less that 10.