-
Notifications
You must be signed in to change notification settings - Fork 639
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
leetcode105:从前序与中序遍历序列构造二叉树 #41
Labels
Comments
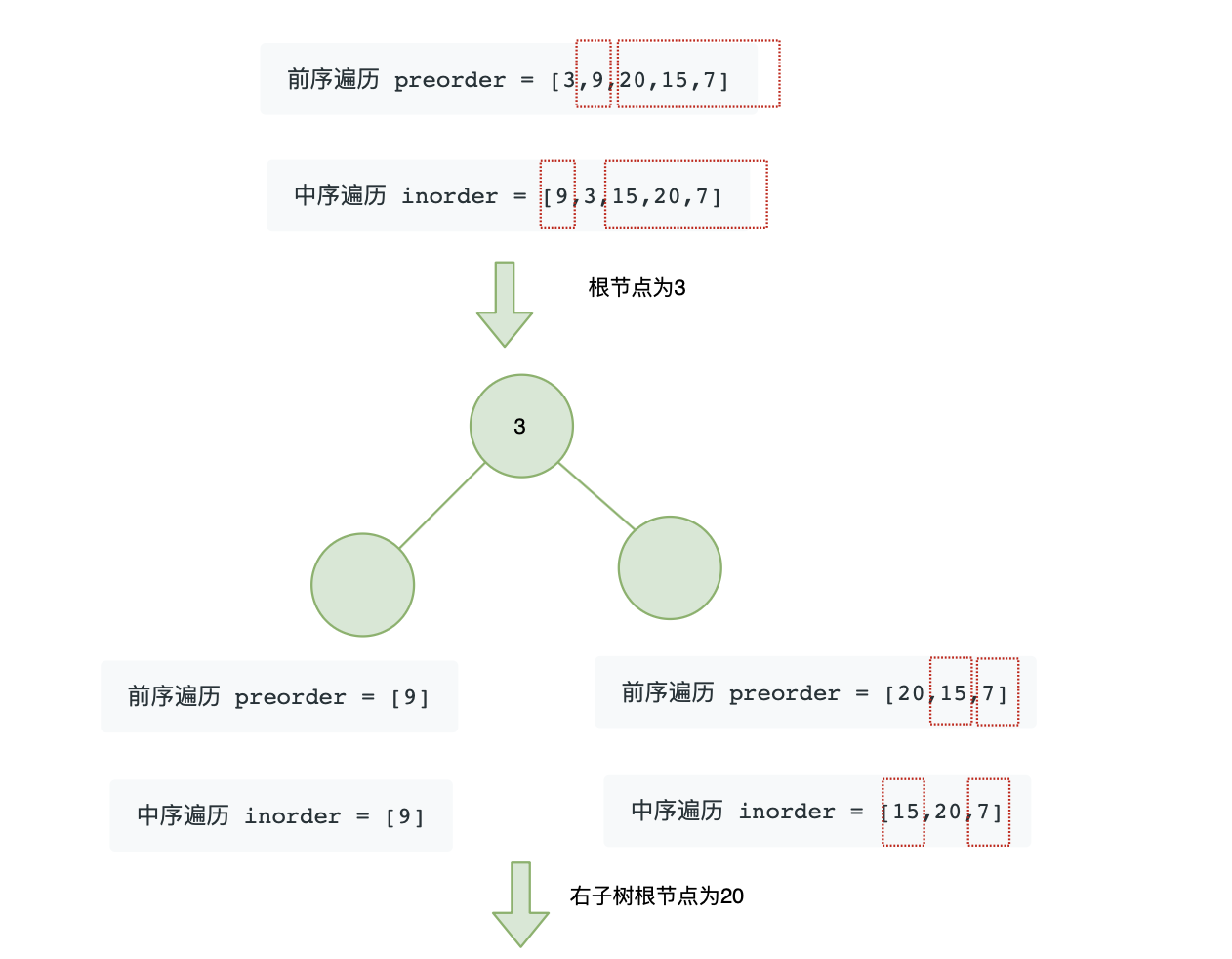
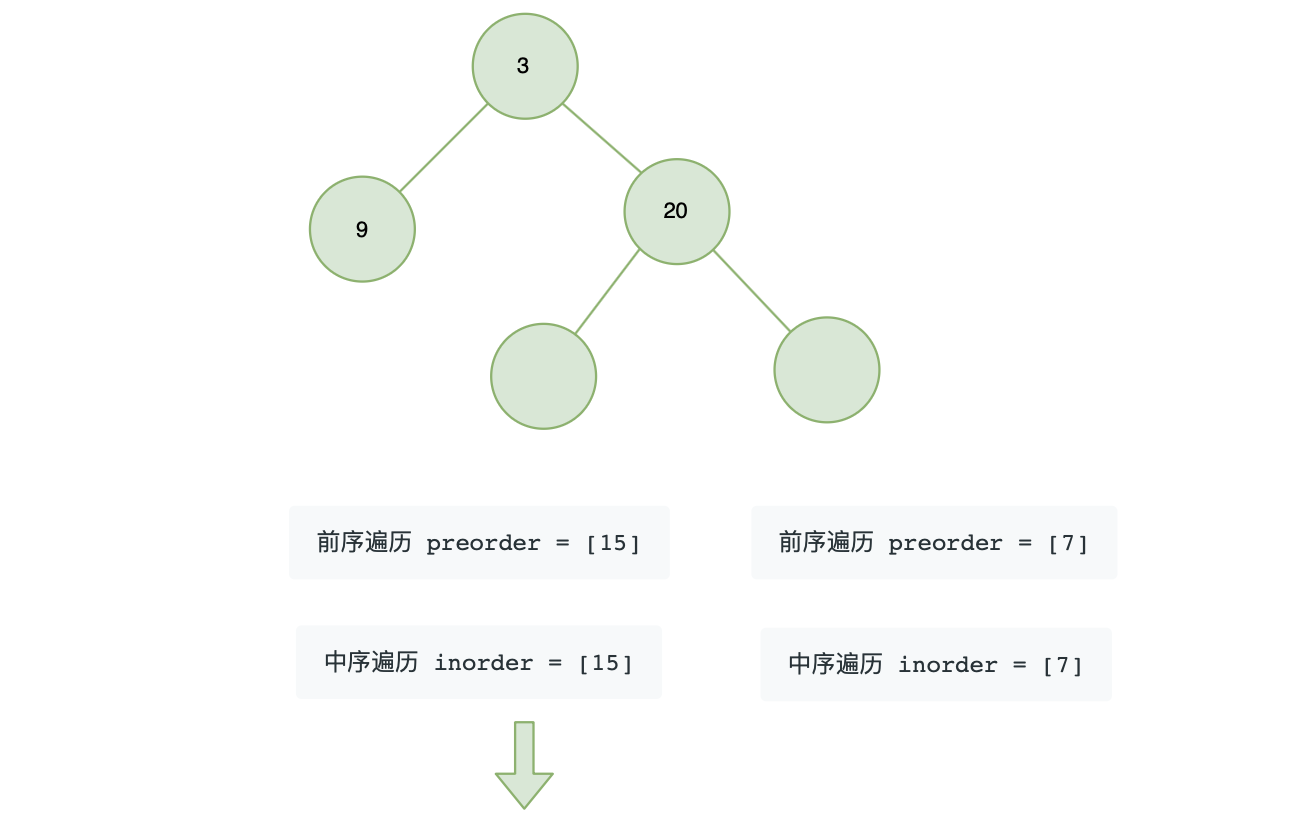
解法:递归法前序遍历:根左右 中序遍历:左根右 我们通过前序遍历可以知道二叉树的根 知道二叉树的根,根据中序遍历,我们可以知道根的左右子树的中序遍历及左右子树节点数目 知道左右子树的节点数目,结合前序遍历,我们就知道左右子树的前序遍历 var buildTree = function(preorder, inorder) {
if(!preorder.length) return null
const node = new TreeNode(preorder[0])
const index = inorder.indexOf(preorder[0])
const inLeft = inorder.slice(0, index)
const inRight = inorder.slice(index + 1)
const preLeft = preorder.slice(1, index + 1)
const preRight = preorder.slice(index + 1)
node.left = buildTree(preLeft, inLeft)
node.right = buildTree(preRight, inRight)
return node
}; |
|
仔细分析前序遍历和中序遍历可以知道(以题目为例):
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
var buildTree = function (preorder, inorder) {
if (preorder.length) {
let head = new TreeNode(preorder.shift());
let index = inorder.indexOf(head.val);
head.left = buildTree(
preorder.slice(0, index),
inorder.slice(0, index)
);
head.right = buildTree(preorder.slice(index), inorder.slice(index + 1));
// 这里要注意,preorder前面shift一次长度比inorder小1
return head;
} else {
return null;
}
}; |
解法:二叉树的前序遍历和中序遍历二叉树的前序遍历中,第一个数字是二叉树的根节点。在中序遍历中,根节点位于序列的中间,即根节点的左边是左子树节点的值,右边是右子树节点的值。 由前序遍历 /**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
var buildTree = function(preorder, inorder) {
if(!preorder.length || !inorder.length) {
return null
}
const rootVal = preorder[0]
const node = new TreeNode(rootVal)
// i有两个含义,一个是根节点在中序遍历结果中的下标, 另一个是当前左子树的节点个数
let i = 0;
for(; i < inorder.length; ++i) {
if(inorder[i] === rootVal) {
break;
}
}
// i主要是求出根节点在中序遍历序列中的位置。那么i位置前面的都是左子树的值,后边的都是右子树的值。
// 中序遍历和前序遍历的左子树和右子树节点的个数都分别相等
// preorder.slice(1, i+1) 在前序遍历里面,左节点有多少个
// inorder.slice(0, i) 在中序遍历里面,左节点就是根节点位置i前面的那些
node.left = buildTree(preorder.slice(1, i+1), inorder.slice(0, i))
node.right = buildTree(preorder.slice(i+1), inorder.slice(i + 1))
return node
}; |
var buildTree = (preorder, inorder) => {
let map = new Map()
for (let i = 0; i < inorder.length; i++) {
map.set(inorder[i], i)
}
return helper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, map)
}
function helper(preorder, p_start, p_end, inorder, i_start, i_end, map) {
if (p_start > p_end) return null // preorder为空
let rootVal = preorder[p_start] // 根节点的值
let root = new TreeNode(rootVal) // 根节点
let mid = map.get(rootVal) // 根节点在inorder的位置
let leftNum = mid - i_start // 左子树的节点数
root.left = helper(preorder, p_start + 1, p_start + leftNum, inorder, i_start, mid - 1, map)
root.right = helper(preorder, p_start + leftNum + 1, p_end, inorder, mid + 1, i_end, map)
return root
} |
var buildTree = function(preorder, inorder) {
if (preorder.length === 0) return null; // 在数组长度为0时结束递归
const root = new TreeNode(preorder[0]); // 前序遍历第一个元素为根节点
const mid = inorder.indexOf(preorder[0]); // 获取根节点中序遍历中的索引
// 根据索引来切割数组 对子数数组继续递归
root.left = buildTree(preorder.slice(1, mid + 1), inorder.slice(0, mid));
root.right = buildTree(preorder.slice(mid + 1), inorder.slice(mid + 1));
return root;
};相似题型leetcode106. 从中序与后序遍历序列构造二叉树 var buildTree = function(inorder, postorder) {
if(!inorder.length) return null // 在数组长度为0时结束递归
const n = postorder.length
const root = new TreeNode(postorder[n-1]) // 中序遍历最后一个元素为根节点
const mid = inorder.indexOf(postorder[n-1]) // 获取根节点后序遍历中的索引
// 根据索引来切割数组 对子数数组继续递归
root.left = buildTree(inorder.slice(0,mid),postorder.slice(0,mid))
root.right = buildTree(inorder.slice(mid + 1),postorder.slice(mid,n-1))
return root
}; |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
注意:
你可以假设树中没有重复的元素。
例如,给出
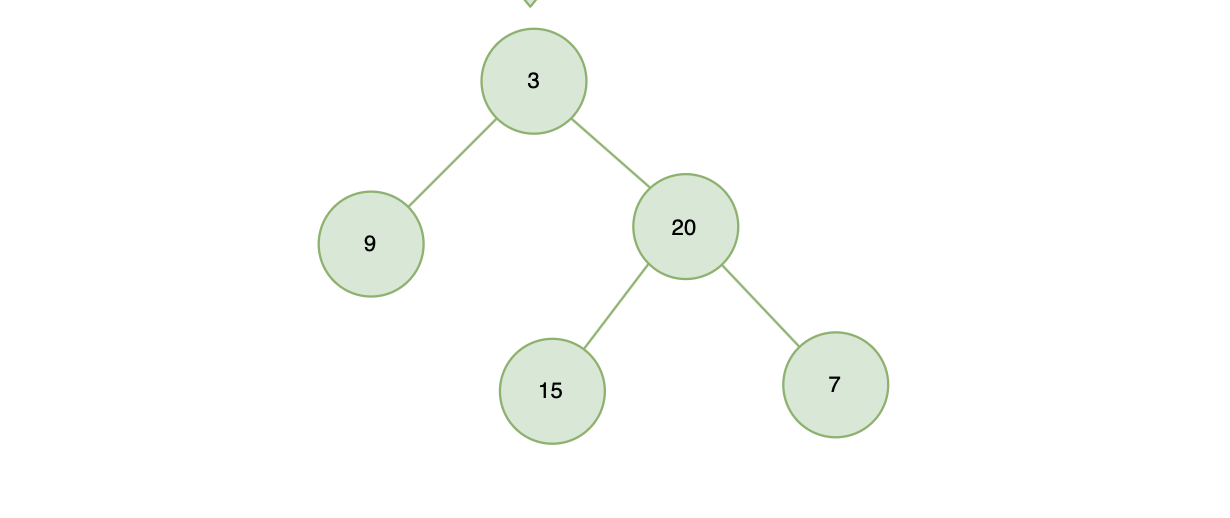
返回如下的二叉树:
限制:
0 <= 节点个数 <= 5000附赠leetcode地址:leetcode
The text was updated successfully, but these errors were encountered: