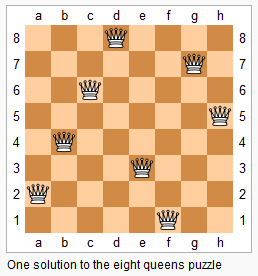
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
示例:
输入: 4 输出: 2 解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
提示:
皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一或 N-1 步,可进可退。(引用自 百度百科 - 皇后 )
n皇后问题我想跟着我们打卡的铁铁们都应该刷烂了,核心思路就是模拟试探,典型的回溯算法,如果八皇后还不会的请看这篇:回溯算法 | 追忆那些年曾难倒我们的八皇后问题 。
对于本题和上一题相比略有区别之处,就是让你输出满足条件的迷宫,这个也很容易啊,在执行回溯的时候维护一个字符型数组,满足条件时候将字符数组。
实现代码为:
boolean shu[];
boolean zuoxie[];
boolean youxie[];
int count=0;
public int totalNQueens(int n) {
shu=new boolean[n];
zuoxie=new boolean[n*2-1];
youxie=new boolean[n*2-1];
dfs(0,n);
return count;
}
//行 map地图
private void dfs(int index,int n) {
// TODO Auto-generated method stub
if(index==n)//存入
{
count++;
}
else {
for(int j=0;j<n;j++)
{
if(!shu[j]&&!zuoxie[index+j]&&!youxie[index+(n-1-j)])
{
shu[j]=true;
zuoxie[index+j]=true;
youxie[index+(n-1-j)]=true;
dfs(index+1, n);
shu[j]=false;
zuoxie[index+j]=false;
youxie[index+(n-1-j)]=false;
}
}
}
}