3-线性模型.md

tags
ML ML/西瓜书 ML/线性模型 ML/对数几率回归

3.1-基本形式

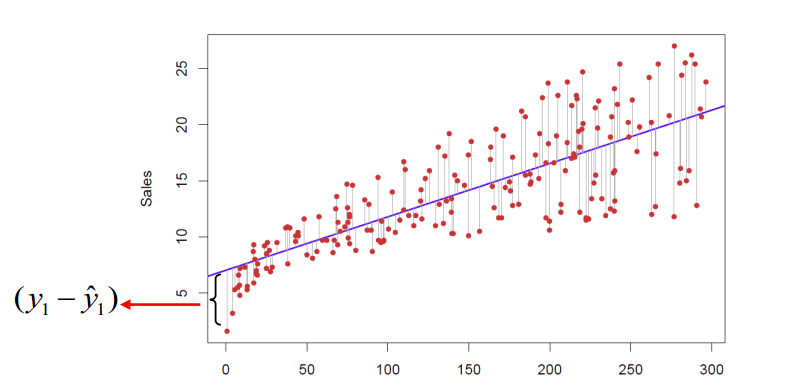
画出一条直线，来拟合数据点

3.1.1-基本形式

$$ f(x) = w_1 x_1 + w_2 x_2 + \dots + w_d x_d + b \tag{3.1} $$

其中 $x$ 为一共 $d$ 个属性的示例，$x_i$ 为 $x$ 的第 $i$ 个属性。$f(x)$ 为预测函数。$w$可以代表各属性在预测中的重要性

3.1.1-向量形式

$$ f(x) = w^Tx+b\tag{3.2} $$

3.2-线性回归

给定数据集 $D = {(x_1,y_1), (x_2, y_2), \dots (x_d, y_d)}$，其中 $x_i = (x_{i1}; x_{i2};\dots;x_{id})$，$y\in \mathbb{R}$

线性回归试图习得一个预测函数 $f(x_i) = w x_i + b$

使得 $$ f(x_i) \simeq y_i\tag{3.3} $$

也就是偏差最小。

3.2.1-性能度量

至于如何确定 $w$ 和 $b$，

2.3 节介绍过，均方误差(2.2) 是回归任务中最常用的性能度量，因此我们可试图让均方误差最小化

$$ \begin{aligned} \left(w^{}, b^{}\right) &=\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} \ &=\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} . \end{aligned}\tag{3.4} $$

最后用最小二乘法解得 $$ w=\frac{\sum_{i=1}^{m} y_{i}\left(x_{i}-\bar{x}\right)}{\sum_{i=1}^{m} x_{i}^{2}-\frac{1}{m}\left(\sum_{i=1}^{m} x_{i}\right)^{2}} \tag{3.7} $$

$$ b=\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-w x_{i}\right) \tag{3.8} $$

这个方法也叫作最小二乘估计。

3.2.2-多元线性回归

更一般的情形是如本节开头的数据集 $D$ ， 样本由 $d$ 个属性描述.此时我们 试图学得 $$ f\left(\boldsymbol{x}{i}\right)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}{i}+b \text {, 使得 } f\left(\boldsymbol{x}{i}\right) \simeq y{i} $$ 这称为“多元线性回归”

把数据集 $D$ 表示为一个 $m \times (d + 1)$ 大小的矩阵 $X$

$$ \mathbf{X}=\left(\begin{array}{ccccc} x_{11} & x_{12} & \ldots & x_{1 d} & 1 \ x_{21} & x_{22} & \ldots & x_{2 d} & 1 \ \vdots & \vdots & \ddots & \vdots & \vdots \ x_{m 1} & x_{m 2} & \ldots & x_{m d} & 1 \end{array}\right)=\left(\begin{array}{cc} \boldsymbol{x}{1}^{\mathrm{T}} & 1 \ \boldsymbol{x}{2}^{\mathrm{T}} & 1 \ \vdots & \vdots \ \boldsymbol{x}_{m}^{\mathrm{T}} & 1 \end{array}\right) $$

$Y$ 写成：$y = (y_1;y_2;\dots;y_m)$

那么： $$ \hat{\boldsymbol{w}}^{*}=\arg \min (\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}}) \tag{3.9} $$ 求导得： $$ \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}}=2 \mathbf{X}^{\mathrm{T}}(\mathbf{X} \hat{\boldsymbol{w}}-\boldsymbol{y}) \tag{3.10} $$

若$X$为正定矩阵或者满秩矩阵，可以直接解得 $$ \hat{w}^* = (X^TX)^{-1} X^T Y $$

反之能够解出很多个 $\hat{w}$

这个时候需要正则化处理

3.2.3-广义线性模型

在这里，我们不会逼近 $y$，反而逼近$y$的某个函数，如 $\ln{y}$ 或者 $y^2$

一般表示成： $$ y = g^{-1}(w^Tx+b) $$

3.3-对数几率回归

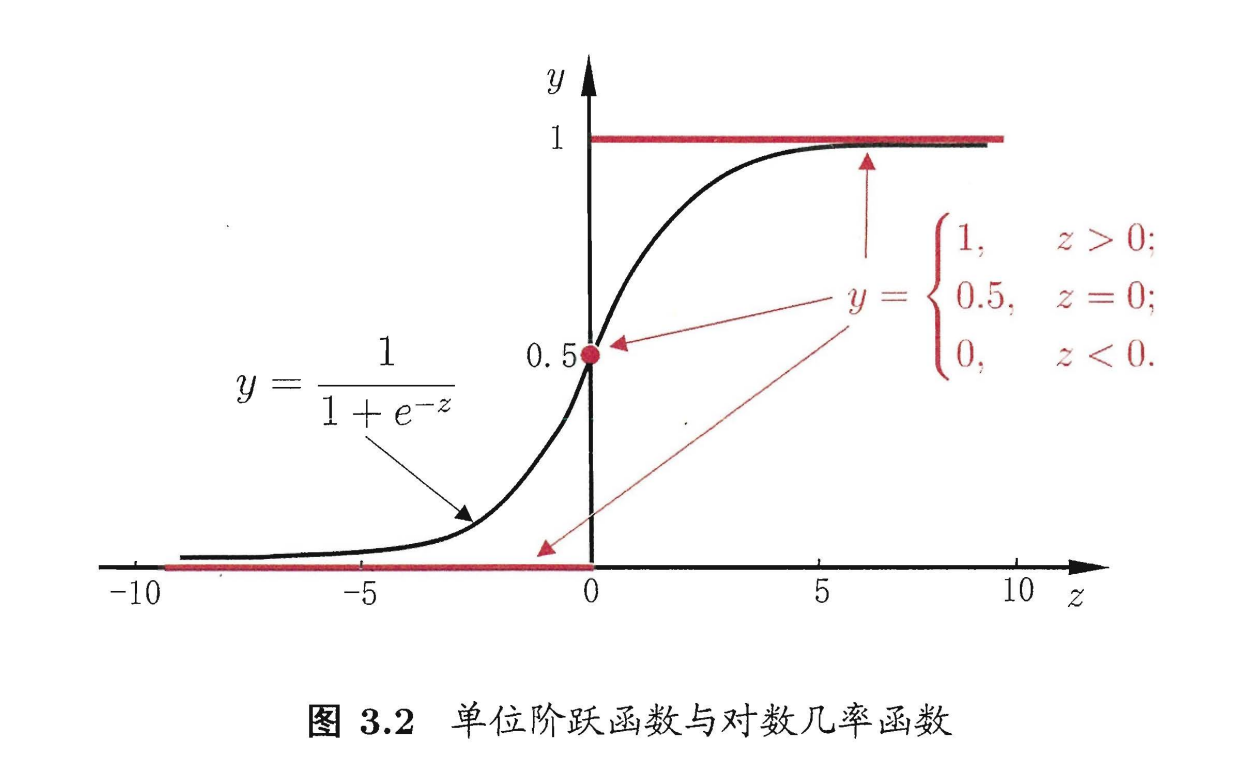
假设现有一模型(其实叫单位阶跃函数) $$ y=\left{\begin{array}{cc} 0, & z<0 \ 0.5, & z=0 \ 1, & z>0 \end{array}\right. \tag{3.16} $$ 这个函数既不连续也不可微¹,那么有没有一个连续可微的替代呢？

有，sigmod函数

其含义是越靠近中心点的概率越高，越远离中心点的概率越低，但是函数预测的确定性越高。

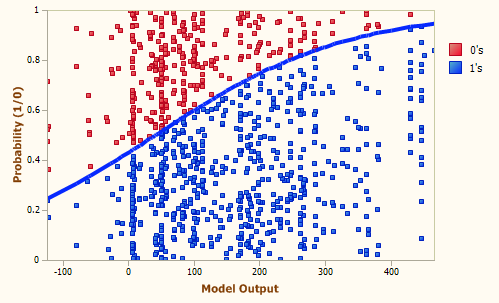
因此, “对数几率回归”(Logistic Regression)做的事情是对分类的可能性建模, 而不是去预测样本的y值²

以下面这张图为例，$x$ 越大，那么预测为蓝色的概率越高，反之越低

3.4-线性判别分析

线性判别分析：Linear Discriminant nalys ，简称 LDA

其思想是：最大化类间均值，最小化类内方差。意思就是将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远³。

3.5-多分类学习

对于多个分类的问题，可以将多分类问题转化为多个二分类问题

• 一对一：OvO
• 一对多：OvR
• 多对多：MvM

MvM的正反类构造有特殊要求

3.5.1-ECOC

纠错输出码：Error Correcting Output Codes

• 编码:对 N 个类别做 M 次划分， 每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集;这样一共产生 M 个训练集，可训练出 M 个分类器.
• 解码:M 个分类器分别对测试样本进行预测，这些预测标记组成一个编码.将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果.

3.6-类别不平衡问题

假设正例有999个，但是反例只有一个，那么只需要将所有的例子都输出为正例行。但是我们其实更加看重那一个反例，而非另外的999个正例。

可以给回归的函数设置权重，原先不是 $\frac{y}{1-y}&gt;1$ 就输出为正例吗？

现在时代变了，需要 $\frac{y}{1-y}&gt;\frac{m^+}{m^-}$ 才能输出为正例，这里的 $m^{+-}$ 代表正例个和反例个数。这称为阔值移动

参考

Footnotes

1. 对数几率回归 —— Logistic Regression - 知乎 (zhihu.com) ↩

2. #8 究竟什么是"逻辑回归", "对数几率回归" ↩

3. 线性判别分析LDA原理及推导过程（非常详细） - 知乎 (zhihu.com) ↩