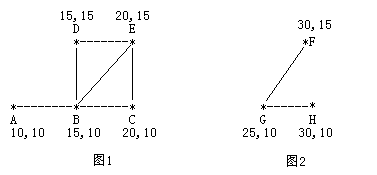农民John的农场里有很多牧区,有的路径连接一些特定的牧区。
一片所有连通的牧区称为一个牧场。
但是就目前而言,你能看到至少有两个牧区不连通。
现在,John想在农场里添加一条路径(注意,恰好一条)。
一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。
考虑如下的两个牧场,每一个牧区都有自己的坐标:
图 1 是有 5 个牧区的牧场,牧区用“*”表示,路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E,它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。
注意,如果两条路径中途相交,我们不认为它们是连通的。
只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,所有牧场(生成的新牧场和原有牧场)中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
第 1 行:一个整数 N, 表示牧区数;
第 2 到 N+1 行:每行两个整数 X,Y, 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行:每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
只有一行,包括一个实数,表示所求答案。
数字保留六位小数。
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
22.071068