Like many sorting algorithms, Merge Sort is a Divide and Conquer algorithm which divides the array of integers into smaller arrays, recursively sorts them, and then merges the two sorted halves into a full sorted array. Merge Sort is a stable sorting algorithm, meaning that if two elements are equal, they remain in the same relative position after sorting is complete. However, Merge Sort is not in-place since it requires additional storage for merging. The Merge Sort benchmarking program implements both recursive and iterative versions.
The time complexity of both the recursive and iterative versions of Merge Sort is Θ(n logn ) for best-case, average, and worst-case. The array has to be iterated through and halved each time to break it down into smaller subarrays, this occurs Θ(log〖n)〗 times on n elements in the array, leading to Θ(n log〖n)〗 time. Since the same steps occur whether the array is already sorted, the best and worst-case times are the same.
Since the Java Virtual Machine uses a lazy loading process, to ensure accurate reading for benchmarking such as this, a JVM warmup is often required. To do this, I created a static method warmUp() which creates a new integer array of length 20, then runs a loop 100,000 times where each iteration creates 2 new objects, a recursive sort and iterative sort, loads the newly created array with 20 random integers between 1 and 100, then calls both the recursive version and then the iterative version on the same array. Doing this allows the classes to be cached and available faster for the benchmarking report.
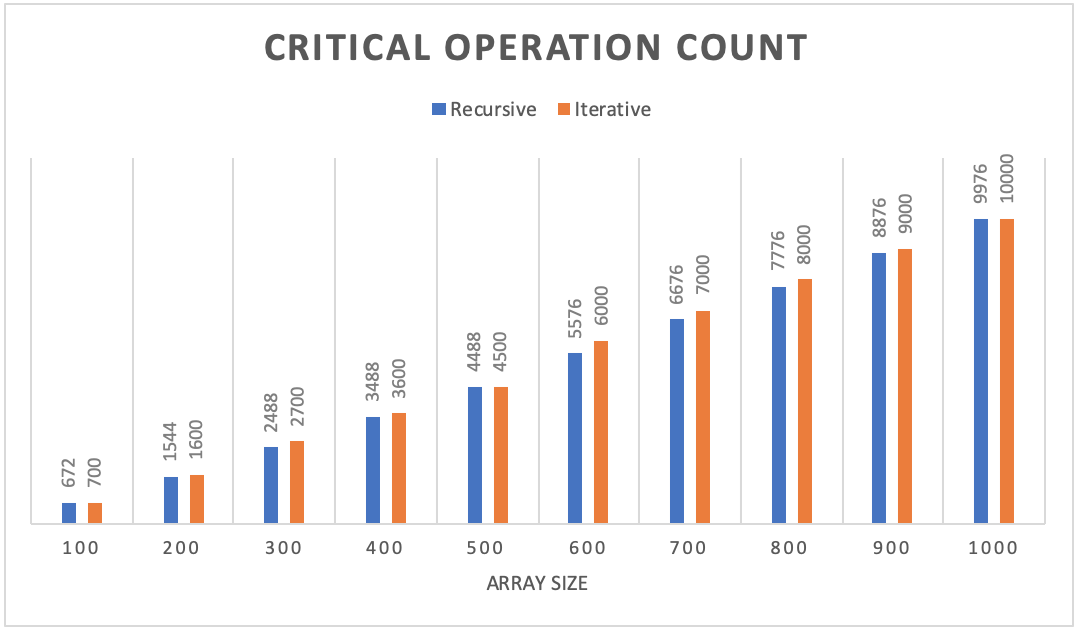
The critical operations I chose to count are the comparisons for sorting and the merge. Once the left and right array have been broken down and sorting and merging can start, that is when the critical operations begin to be counted.
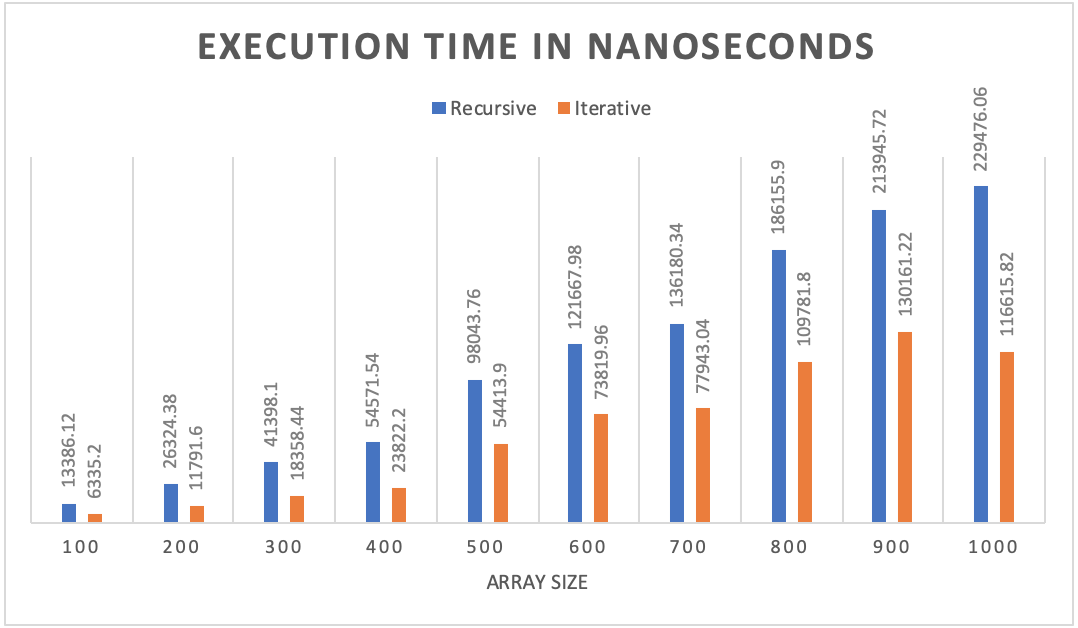
When examining the charts above, we can see that the critical operation count for the recursive and iterative versions is very similar with the recursive version being a little lower than iterative for each of the array sizes. However, the execution time in nanoseconds for the iterative version was about half the execution time of the recursive version. With the iterative version running in half the time with minimal extra counts above the recursive version, this leads me to believe that the iterative version outperformed the recursive version according to these stats.
Calculating the coefficient of variation is a useful statistic for comparing the degree of variation from one data series to another. To calculate the coefficient of variation for both the execution time and critical operation count, we first get the values and calculate the mean from the output files from BenchmarkMergeSort.java. The variance is calculated from adding up the squares of each value minus the mean and dividing by the total number of values. The standard deviation is the square root of the variance. Finally, we can find the coefficient of variation by dividing the standard deviation by the mean. Here are the output reports from both the recursive and iterative versions from BenchmarkReport.java:
We can see from the reports above that the coefficient of variation of the execution times are almost all just under one percent. This shows that all the calculations had very low variation so the benchmarking data should be accurate. Since the time complexity for Merge Sort is the same for the best, worst and average cases, the critical operations are always the same, hence the zero percent coefficient of variation for the critical count.
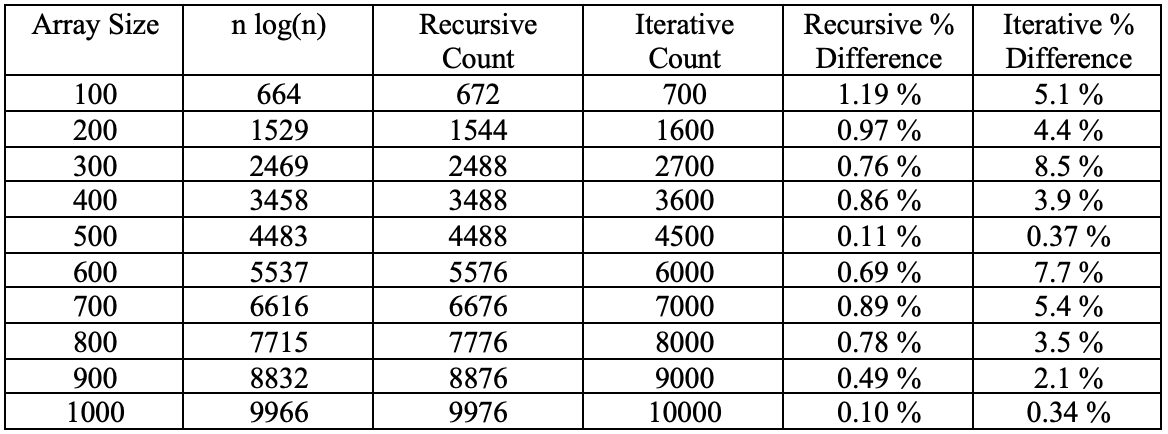
My Big-Θ analysis of Merge Sort above was a time complexity of Θ(n logn). Below is a table showing the n log(n) for each of the array sizes and how that number compares to the recursive and iterative critical operation count. Also shown is the percentage of difference for both versions.
We can see from the table that the recursive version was much closer to the n log(n) value with almost all of them being less than a 1% difference. The iterative version was also close with all counts being under 10% difference but not as close as the recursive version.
When analyzing the output data from the benchmarking program, we can see how the recursive and iterative versions of Merge Sort compare with regards to critical operation counts and actual execution time recorded in nanoseconds. The chart above shows that both versions were similar in critical operation count with the recursive version being a little less than iterative for each of the array sizes. The recursive version was also closer to the actual time complexity of n log(n) being within about 1% for each array size. The iterative version was also close to my Big-Θ analysis but the difference fluctuated more than recursive. While the critical operation count for both versions was similar, the actual execution time for both versions was quite different. The iterative version ran in roughly half the time compared to the recursive version. With the coefficient of variation being only about 1% for the critical operations count of both versions, this led me to believe that my results were accurate and the output data was not widely varied. Since the iterative version had slightly more critical operations performed, yet ran in roughly half the time of the recursive version, I would conclude that iterative version of Merge Sort outperformed the recursive version according to these statistics.