先复习一下TreeMap
时间复杂度(平均):添加、删除、搜索:O(logn)
特点 :
- Key 必须具备可比较性
- 元素的分布是有顺序的
在实际应用中,很多时候的需求 Map 中存储的元素不需要讲究顺序
Map 中的 Key 不需要具备可比较性
不考虑顺序、不考虑 Key 的可比较性,Map 有更好的实现方案,平均时间复杂度可以达到 O(1) ,那就是采取哈希表来实现 Map
现在我们有一个需求
- 需要设计一个写字楼通讯录,存放所有公司的通讯信息
- 座机号码作为 key(假设座机号码最长是 8 位),公司详情(名称、地址等)作为 value
- 添加、删除、搜索的时间复杂度要求是 O(1)
显然底层是红黑树的数据结构TreeMap不能满足我们的需求,这个时候我们可以考虑用数组存,写一下伪代码
电话号码是不可能重复,这样做法的时间复杂度为O(1),满足要求!
private Company[] companies = new Company[100_000_000];
public void add(int phone ,Company company){
companies[phone] = company;
}
public void remove(int phone){
companies[phone] = null;
}
public Company get(int phone){
return companies[phone];
}但是这样有什么问题吗?当然有,问题大了
- 空间复杂度非常大
- 空间使用率极其低,非常浪费内存空间
- 其实数组 companies 就是一个哈希表,典型的【空间换时间】
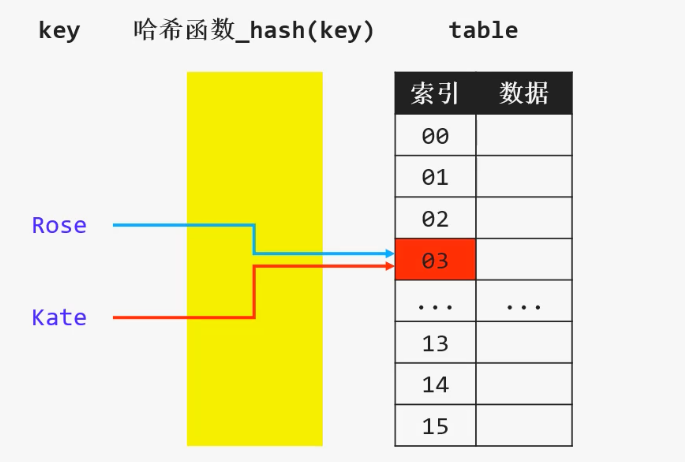
哈希冲突也叫做哈希碰撞,指的是2 个不同的 key,经过哈希函数计算出相同的结果
例如:key1 ≠ key2 ,hash(key1) = hash(key2)
解决Hash冲突的方式有很多,这里介绍几种常见的方法
-
开放定址法(Open Addressing)
按照一定规则向其他地址探测,直到遇到空桶。一般有线性探测和平方探测两种,线性探测即如果遇到冲突,往下寻址,直到找到空余位置为止;平方探测即按照第一次为1^2,第二次往下2^2,...的方式往下寻址
-
再哈希法(Re-Hashing)
设计多个哈希函数。如果hash冲突,可以换一种hash函数进行hash
-
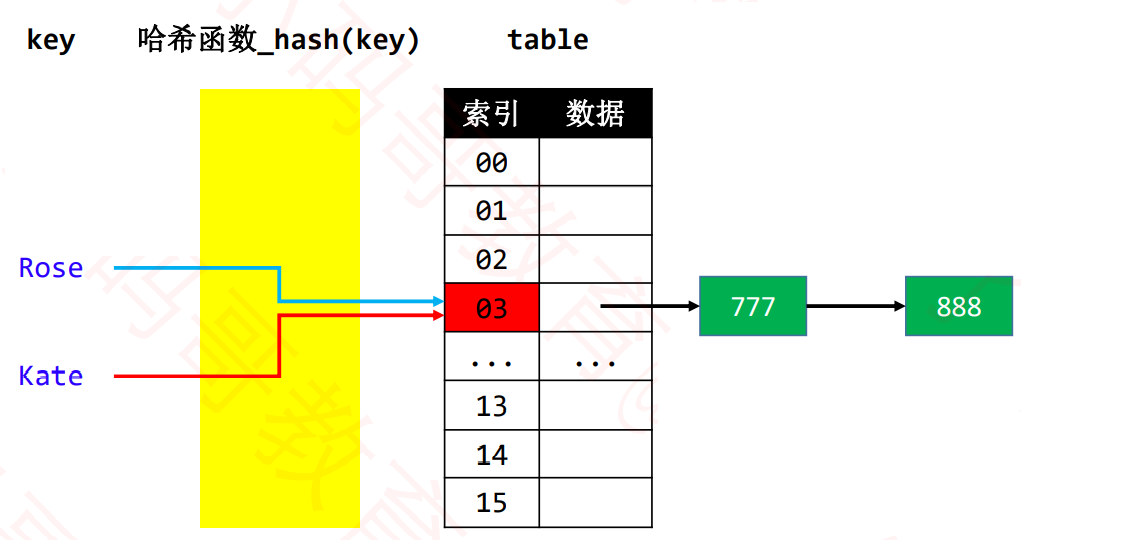
链地址法(Separate Chaining)
比如通过链表将同一index的元素串起来
jdk解决方案:
- 默认使用单向链表将元素串起来
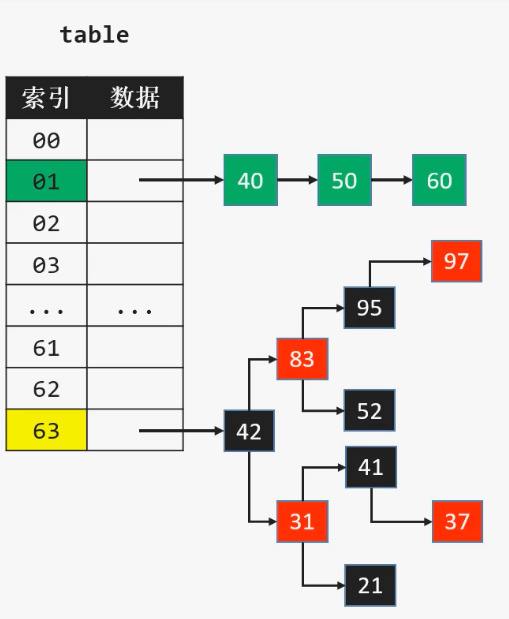
- 在添加元素时,可能会由单向链表转为红黑树来存储元素
- 当红黑树节点数量少到一定程度时,又会转为单向链表
结论:JDK1.8中的哈希表是使用链表+红黑树解决哈希冲突
那么为什么使用单链表,而不是双向链表呢?
- 每次都是从头节点开始遍历
- 单向链表比双向链表少一个指针,可以节省内存空间
那么上面是hash值呢?其实hash值就是一串整数
哈希表中哈希函数的实现步骤大概如下:
- 先生成 key 的哈希值(必须是整数)
- 再让 key 的哈希值跟数组的大小进行相关运算,生成一个索引值
public int hash(Object key){
return hash_code(key) % table.length;
}为了提高效率,可以使用 & 位运算取代 % 运算【前提:将数组的长度设计为 2 的幂(2 ^ n)】
public int hash(Object key){
return hash_code(key) & (table.length - 1);
}接下来我们研究一下为什么数组长度必须是2的n次方,明明 & 位运算与取模运算 % 完全不一样
首先我们看一下2 ^ n,由大学计组可知以下等式成立😁
-------------------------------
二进制位 | 2^n
1 | 2^0
10 | 2^1
100 | 2^2
1000 | 2^3
... | 2^n
------------------------------- 那么如果是2 ^ n - 1呢?
-------------------------------
二进制位 | 2^n
0 | 2^0 - 1
01 | 2^1 - 1
011 | 2^2 - 1
0111 | 2^3 - 1
... | 2^n - 1
------------------------------- 是不是相当于原来的二进制位做了一次取反操作,然后2的多少次方减一就相当于与有多少了1
所以如果我们规定table.length - 1,那么它一定全部都是1,这一点非常的重要
那么hash_code(key),也就是k的hash值,与上一个全是1的家伙是什么情况呢?我们观察一下,这里我们假设一个hash值
1001011
& 1111111
1001011你会发现相同位的数还是本身!并且我们得出的结果一定小于table.length - 1,显然我们没法大过全是1的家伙,显然是把高位丢弃了,并且小于数组的长度,这样其实就可以保证hash后的位置一定在数组内,并且其实这里还埋下了一个伏笔!非常的精彩🎈
1001011
& 0001111
0001011对于上面的 & 运算取代 % 运算的奥秘,如果只是因为确保元素都能够正常进入我们的数组,那么这也太过于肤浅了,HashMap的魅力不止于此,等我们手写到HashMap扩容逻辑的时候,我们再来看这个伏笔🤞
其实我们用 % 运算计算索引也是可以的,但是我们需要注意以下的几点规则
- 建议把哈希表的长度设计为素数(质数)
- 可以大大减小哈希冲突
右边表格列出了不同数据规模对应的最佳素数,特点如下:
- 每个素数略小于前一个素数的2倍
- 每个素数尽可能接近2的幂(2 n)
| 除数为偶数 | 除数为质数 |
|---|---|
| 10%8 = 2 | 10%7 = 3 |
| 20%8 = 4 | 20%7 = 6 |
| 30%8 = 6 | 30%7 = 2 |
| 40%8 = 0 | 40%7 = 5 |
| 50%8 = 2 | 50%7 = 1 |
| 60%8 = 4 | 60%7 = 4 |
| 70%8 = 6 | 70%7 = 0 |
这里其实我们有一个最佳实践:
key 的常见种类可能有:
整数、浮点数、字符串、自定义对象 。不同种类的 key,哈希值的生成方式不一样,但目标是一致的
- 尽量让每个 key 的哈希值是唯一的
- 尽量让 key 的所有信息参与运算
在Java中,HashMap 的 key 必须实现 hashCode、equals 方法,也允许 key 为 null
我们知道hash值为整数,那么如果我们传入的就是整数怎么办呢?
- 整数值当做哈希值
- 比如 10 的哈希值就是 10
我们可以这样实现(注意jdk中并不是这样做的,这里仅提供一种思想)
public int hash(int value){
return value;
}当我们的value为浮点数时,我们需要先知道,一个浮点数在计算机中是如何表示的,由计组可知:
------------------------------------------------------
浮点数(float) | 二进制数
8.8 | 01000001000011001100110011001101
------------------------------------------------------底层其实还是二进制数,具体转化的过程请复习大学的计算机组成原理
这里我们处理浮点数的做法是:将存储的二进制格式转为整数值
public int hashCode(float value){
return Float.floatToIntBits(value);
}floatToIntBits是将float转为二进制bit,并以十进制输出,这里刚好就是我们想要的int类型
可能我们会想这不是和int类型一样吗?直接将其作为hash值不就好了,但是java规定hash只能是32位的
有两种做法:取前32位或者取后32位,但是这样都不好,因为hash应该尽可能计算key的所有部分
我们这里看看java官方的做法:
public int hashCode(long value){
return (int)(value ^ (value >>> 32));
}public int hashCode(double value){
// 先转为bit,由于double是64位,所以输出long
long bits = Double.doubleToLongBits(value);
return (int)(value ^ (bits >>> 32));
}那这里的 >>> 和 ^ 的作用是什么呢?>>> 表示无符号右移,^ 表示异或运算,我们在计算机组成原理里面学过,一个数字的第一位表示符号位,0表示正数,1表示负数。而异或表示相异为1,相同为0;对应同或表示,相同为1,相异为0
Java中 >> 和 >>> 的区别
>>:带符号右移。正数右移高位补0,负数右移高位补1。比如:
4 >> 1,结果是2;-4 >> 1,结果是-2。-2 >> 1,结果是-1。
>>>:无符号右移。无论是正数还是负数,高位通通补0。
对于正数而言,>>和>>>没区别。
对于负数而言,-2(11111111 11111111 11111111 11111110) >>> 1(01111111 11111111 11111111 11111111),结果是2147483647(Integer.MAX_VALUE),-1 >>> 1,结果是2147483647(Integer.MAX_VALUE)。
所以,要判断两个数符号是否相同时,可以这么干:
return ((a >> 31) ^ (b >> 31)) == 0;其实是用高32bit 和 低32bit 混合计算出 32bit 的哈希值,我们也将这种操作称为扰动计算,这里非常重要,面试必考
这也遵循了我们的准则,要充分利用所有的熟悉计算hash值,不能只取高32位或者低32位!
假设现在给我们一个64位的value,如下图所示:
我们这样分析这个栗子,当value无符号右移32位后,高32位填充0,真正的高32位现在在低32位的地方,现在我们再和原来的value进行异或运算,显然就是double本身的高32位与低32位进行了运算(异或),这正好符合java的两个规范:
- java规定hash运算的结果只能是32位的
- 要充分利用key的所有值进行运算(不能抛掉一部分)
当我们算出来后,再强制转为int类型,即直接将高32位抛弃,只取后面黄色的那一串数字
那为什么这里要用异或运算呢?不可以使用与、或、非运算吗?不可以使用同或运算吗?
其实我们仔细观察会发现:
- 如果采用&运算计算出来的值会向0靠拢(00,01,10,11:前三种情况做&操作都是得到0,只有11才为1)
- 采用|运算计算出来的值会向1靠拢
采用高16位异或低16位的最终目的还是为了让哈希后的结果更均匀的分布,减少哈希碰撞,提升hashmap的运行效率
字符串是如何计算hash值的呢?我们知道hash值是32位的数字,我们先来看一下下面的小案例
问:整数 5489 是如何计算出来的?
5 * 10^3 + 4 * 10^2 + 8 * 10^1 + 9 * 10^0 = 5489 同理我们知道:字符串是由若干个字符组成的
比如字符串 jack,由 j、a、c、k 四个字符组成(字符的本质就是一个整数)
因此,jack 的哈希值可以表示为 j ∗ n^3 + a ∗ n^2 + c ∗ n^1 + k ∗ n^0
这里给出上面式子的等价公式: [ ( j ∗ n + a ) ∗ n + c ] ∗ n + k
上面的例子因为是十进制,所以n取10,那么计算字符串可以去字符的个数做底数,例如如果是字母,n取26即可
- 在JDK中,乘数 n 为 31,为什么使用 31?
这里牵涉到很多数学的东西,这里先给出结论:31 是一个奇素数,JVM会将 31 * i 优化成 (i << 5) – i
原因大致有:
- 31不仅仅是符合2^n – 1,它是个奇素数(既是奇数,又是素数,也就是质数)
- 素数和其他数相乘的结果比其他方式更容易产成唯一性,减少哈希冲突
- 最终选择31是经过观测分布结果后的选择
上面的等价公式中显然有很多n的乘操作,n取31,JVM会将其优化,这样效率更高,所以n取31
这里我们写一个小栗子,计算
jack的hashcode
public class TestHash {
public static void main(String[] args) {
String str = "jack";
int len = str.length();
int hashCode = 0;
for (int i = 0; i < len; i++) {
char c = str.charAt(i);
hashCode = hashCode * 31 + c;
// hashCode = (hashCode << 5) - hashCode + c;
}
System.out.println(hashCode); //3254239
System.out.println(str.hashCode()); //3254239
}
}可以看出Java官方的做法是和我们一模一样的😏
我们总结一下不同类型去hash值的方法:
显然Java官方和我们的做法一模一样😏
@Test
public void test02() {
Integer integer = 18;
Float _float = 18.0f;
Double _double = 18.0;
Long _long = 18L;
String str = "rose";
System.out.println(integer.hashCode()); // 18
System.out.println(_float.hashCode()); // 1099956224
System.out.println(_double.hashCode()); // 1077018624
System.out.println(_long.hashCode()); // 18
System.out.println(str.hashCode()); // 3506511
}我们先来看一下面的代码:
其实可以看到,对象的hash值其实默认是与该对象内存地址有关
Person p1 = new Person(18, 1.67f, "张三");
Person p2 = new Person(18, 1.67f, "张三");
System.out.println(p1.hashCode());// 460141958
System.out.println(p2.hashCode());// 1163157884
Map<Object,Object> map = new HashMap<>();
map.put(p1,"abc");
map.put(p2,"def");// map.size() = 2;但是我们一般的业务场景是只要属性字段一样就认为这两个对象相等,第二次存的时候就应该覆盖第一次的字段
这时候我们需要重写hashcode方法,这样也是充分利用了所有的属性
@Override
public int hashCode() {
int hashCode = Integer.hashCode(age);
hashCode = hashCode * 31 + Float.hashCode(height);
hashCode = hashCode * 31 + (name == null ? 0 : name.hashCode());
return hashCode;
}重写hashcode后我们也需要重写一下equels方法,在hash冲突后进行key的比较
@Override
public boolean equals(Object o) {
// 是一样的对象,直接返回
if (this == o) return true;
// 为空或者类文件不一样
if (o == null || getClass() != o.getClass()) return false;
// 比较成员变量,成员变量一样即相等
Person person = (Person) o;
return age == person.age &&
Float.compare(person.height, height) == 0 &&
Objects.equals(name, person.name);
}总结一下:hashCode方法在计算索引的时候使用,equels方法在发生hash冲突后比较key
我们在使用自定义对象作为key的时候,可能会调用对象的equals方法,但是如果出现下面的这种情况会怎么样呢?
// 假设有两个对象 obj1 和 obj2
obj1.equals(obj2) // true
obj2.equals(obj1) // false 出现这种情况,显然是写equals的同学没有遵循好equals的规定,equals规定有:
- 自反性:对于任何非 null 的 x,x.equals(x)必须返回true
- 对称性:对于任何非
null的 x、y,如果 y.equals(x) 返回true,x.equals(y) 必须返回true - 传递性:对于任何非
null的 x、y、z,如果 x.equals(y)、y.equals(z) 返回true,那么x.equals(z) 必须 返回true - 一致性:对于任何非
null的 x、y,只要 equals 的比较操作在对象中所用的信息没有被修改,多次调用 x.equals(y) 就会一致地返回true,或者一致地返回false - 对于任何非
null的 x,x.equals(null) 必须返回false
hashCode :必须保证 equals 为 true 的 2 个 key 的哈希值一样,反过来 hashCode 相等的 key,不一定 equals 为 true
不重写 hashCode 方法只重写 equals 会有什么后果?
可能会导致 2 个 equals 为 true 的 key 同时存在哈希表中
这里我们先实现以下的方法,扩容的方法先不进行实现:
int size();
boolean isEmpty();
void clear();
V put(K key, V value);
V get(K key);
V remove(K key);
boolean containsKey(K key);
boolean containsValue(V value);
void traversal(Visitor<K, V> visitor);和TreeSet一样,我们让其继承Map接口
/**
* Map 接口
* @param <K>
* @param <V>
* @since 2022年7月12日
* @author 梁峰源
*/
public interface Map<K, V> {
int size();
boolean isEmpty();
void clear();
V put(K key, V value);
V get(K key);
V remove(K key);
boolean containsKey(K key);
boolean containsValue(V value);
void traversal(Visitor<K, V> visitor);
abstract class Visitor<K, V> {
public boolean stop;
public abstract boolean visit(K key, V value);
}
}我们知道在jdk1.8中HashMap采用的是数组+链表+红黑树,当链表的高度高于8转为红黑树,当链表长度矮于6转为链表,这里我们先以红黑树来实现,即每个桶位置后面都会放红黑树的根结点。
这里需要红黑树的先导知识,可以看笔者之前TreeMap和红黑树的文章,这里直接使用了
这里我们需要在结点里面添加一些信息,例如hashCode,每个结点都应该用key计算出hashCode,方便后面红黑树进行比较并且减少hashCode的计算次数
private static final boolean RED = false;
private static final boolean BLACK = true;
// 红黑树结点
private static class Node<K, V> {
K key;
V value;
int hashCode; // 保存hashCode
boolean color = RED;
public Node<K, V> left;//左结点
public Node<K, V> right;//右结点
public Node<K, V> parent;//父结点
public Node(K key, V value, Node<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
this.hashCode = key == null ? 0 : key.hashCode();
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
public boolean isRightChild() {
return parent != null && this == parent.right;
}
// 返回当前结点的兄弟结点
public Node<K, V> sibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
//没有兄弟结点
return null;
}
}红黑树结点我们定义出来了,那么我们可以想到,我们HashMap的数组其实就是一个Node数组,即将红黑树的根结点放在数组对应的位置,我们先在先定义这个数组
Node<K,V>[] table;我们在这里可以先写一点代码
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
if (table != null && size > 0) {
size = 0;
// 遍历每个桶,将头结点置空
for (int i = 0; i < table.length; ++i)
table[i] = null;
}
}接下来我们需要计算传入key的hashCode了
/**
* 计算Key的索引
*/
private int index(K key){
// HashMap运行key为空,为空我们将其放到数组下标为0的位置
if(key == null) return 0;
// 计算hashCode
int hashCode = key.hashCode();
// 拿高16位和低16位进行混淆运算,让hash值更加离散,减少hash冲突
hashCode = hashCode ^ (hashCode >>> 16);
return hashCode & (table.length -1);
}HashMap底层就是一棵红黑树,所以这里我们需要将之前红黑树的代码搬过来,并且红黑树添加时元素比较的代码我们也要重写一下
这里需要红黑树的先导知识了,如果不知道也没关系,知道我们是用红黑树进行存储的就行
/*--------------HashMap中的key的比较--------------*/
/**
* 规定传入对象的比较规则
*
* @param k1 第一个对象
* @param k2 第二个对象
* @param h1 k1的hash值
* @param h2 k2的hash值
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
@SuppressWarnings("unchecked")
private int compare(K k1, K k2, int h1, int h2) {
// 先比较hash值,如果hash值不同,返回hash值的差
int result = h1 - h2;
if (result != 0) return result;
// hash值一样,需要比较equals
if (Objects.equals(k1, k2)) return 0;
// hash值相等,但不equals,我们比较类名
if (k1 != null && k2 != null) {
String k1ClassName = k1.getClass().getName();
String k2ClassName = k2.getClass().getName();
// 通过类名进行比较
result = k1ClassName.compareTo(k2ClassName);
if (result != 0) return result;
// 类名也相等,继续比较,如果key实现了Comparable接口,直接进行比较
if (k1 instanceof Comparable) return ((Comparable) k1).compar
}
/*
* 同一种类型,但是不具备可比较性
* 1. k1为null但k2不为null
* 2. k2不为null但是k1为空
* 注意:k1、k2都为空的情况已经被上面的Objects.equals方法拦截
*/
// 到了这里,只能比较内存地址了
return System.identityHashCode(k1) - System.identityHashCode(k2);
}
/*------------------修复红黑树性质---------------------*/
/**
* 修复红黑树性质
*/
private void afterPut(Node<K, V> node) {
// 先取出父结点
Node<K, V> parent = node.parent;
// 添加的是根结点(将其染成黑色并返回)或者上溢到根结点
if (parent == null) {
black(node);
return;
}
// 如果是前四种情况,即父结点为黑色结点,不用处理
if (isBlack(parent)) return;
// 取出uncle结点
// 取出祖父结点
Node<K, V> grand = parent.parent;
Node<K, V> uncle = parent.sibling();
// 如果叔父结点是红色【B树结点上溢,只需要染色】
if (isRed(uncle)) {
black(parent);
black(uncle);
// 把祖父结点当做是新添加的结点
// 递归调用
afterPut(red(grand));
return;
}
/*
* 叔父结点不是红色,有四种情况
* LL/RR: parent染成BLACK,grand染成RED - grand进行单旋操作
* LR/RL: 自己染成black,grand染成red,再双旋
*/
if (parent.isLeftChild()) { // L
red(grand);
if (node.isLeftChild()) { // LL
black(parent);
} else { // LR
black(node);
rotateLeft(parent);
}
rotateRight(grand);
} else { //R
red(grand);
if (node.isLeftChild()) { // RL
black(node);
rotateRight(parent);
} else { // RR
black(parent);
}
rotateLeft(grand);
}
}
/**
* 对该元素进行左旋转
*
* @param grand 待旋转的结点
*/
protected void rotateLeft(Node<K, V> grand) {
if (null == grand) return;
//获得parent结点
Node<K, V> parent = grand.right;
//将parent的左子结点取出
Node<K, V> leftChild = parent.left;
//左旋
grand.right = leftChild;
parent.left = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, leftChild);
}
/**
* 对该元素进行右旋转
*
* @param grand 待旋转的结点
*/
protected void rotateRight(Node<K, V> grand) {
//获得parent结点,即grand结点的左结点
Node<K, V> parent = grand.left;
//获得parent结点的右子结点,方便后面更新高度
Node<K, V> rightChild = parent.right;
//右旋
grand.left = rightChild;
parent.right = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, rightChild);
}
/**
* 旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
*/
protected void afterRotate(Node<K, V> grand, Node<K, V> parent, Node<
/*
* 让parent结点成为当前子树的根结点
* 这里有两步:
* 1. 让parent的父结点指向grand的父结点
* 2. 让grand父结点本来指向grand的指针指向parent,这里顺便更新了parent结点的父结点
**/
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else {
//当前结点没有父结点,即grand结点就是root结点
table[index(grand.key)] = parent;
}
/*
* 一共需要更新三个结点的parent,grand、parent和leftChild结点
* grand结点在上面第二步中已经更新了,所以这里我们还需要更新parent结点和leftChild结点的parent结点
**/
if (child != null) {
child.parent = grand;
}
//更新grand的parent结点
grand.parent = parent;
}
/**
* 找到当前结点的前驱结点
*/
protected Node<K, V> predecessor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
//前驱结点在左子树当中(left.right.right.......)
Node<K, V> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
/*
* 这里有两种情况
* 1. node.parent == null
* 2. node = node.parent.right;
*/
return node.parent;
}
/**
* 找到其后继结点
*/
protected Node<K, V> successor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
Node<K, V> p = node.right;
//第一种情况,其后继结点为node.right.left.left...
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
/*
* 来到这里有两种情况
* 1. node.right = null
* 2. node = node.parent.left;
*/
return node.parent;
}
//染成红色
private Node<K, V> red(Node<K, V> node) {
return color(node, RED);
}
//染成黑色
private Node<K, V> black(Node<K, V> node) {
return color(node, BLACK);
}
/**
* 将元素染色
*
* @param node 带染色的结点
* @param color 需要染的颜色
* @return 将染色的结点返回
*/
private Node<K, V> color(Node<K, V> node, boolean color) {
if (node == null) return node;
node.color = color;
return node;
}
//查看当前结点颜色
private boolean colorOf(Node<K, V> node) {
return node == null ? BLACK : node.color;
}
private boolean isBlack(Node<K, V> node) {
return colorOf(node) == BLACK;
}
private boolean isRed(Node<K, V> node) {
return colorOf(node) == RED;
}我们知道红黑树是一棵BST,也就是平衡二叉树,那么它的结点一定是要可以比较的,我们的HashMap又是无序的,其实这两者并不冲突,我们需要的是红黑树只是有序,我们可以先写一下红黑树的比较逻辑:
- 先根据hash值进行比较
- hash相同,使用equals进行比较
- equals相同,比较类名
- 类名相同,看有没有带Comparable接口,有就比较
- 比较内存地址
/**
* 规定传入对象的比较规则
*
* @param k1 第一个对象
* @param k2 第二个对象
* @param h1 k1的hash值
* @param h2 k2的hash值
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
private int compare(K k1, K k2, int h1, int h2) {
// 先比较hash值,如果hash值不同,返回hash值的差
int result = h1 - h2;
if (result != 0) return result;
// hash值一样,需要比较equals
if (Objects.equals(k1, k2)) return 0;
// hash值相等,但不equals,我们比较类名
if (k1 != null && k2 != null) {
String k1ClassName = k1.getClass().getName();
String k2ClassName = k2.getClass().getName();
// 通过类名进行比较
result = k1ClassName.compareTo(k2ClassName);
if (result != 0) return result;
// 类名也相等,继续比较,如果key实现了Comparable接口,直接进行比较
if (k1 instanceof Comparable) return ((Comparable) k1).compareTo(k2);
}
/*
* 同一种类型,但是不具备可比较性
* 1. k1为null但k2不为null
* 2. k2不为null但是k1为空
* 注意:k1、k2都为空的情况已经被上面的Objects.equals方法拦截
*/
// 到了这里,只能比较内存地址了
return System.identityHashCode(k1) - System.identityHashCode(k2);
}上面的比较代码似乎已经尽了我们最大的可能去进行比较,看起来好像也没有什么问题,但是其实还是存在很大的问题的
问题就出在如果我们的key是一个对象,现在发生hash冲突,最终其实是依靠内存地址去进行比较
例如我们定义一个类,如下:
public class Key {
protected int value;
public Key(int value) {
this.value = value;
}
@Override
public int hashCode() {
return value / 10;
}
@Override
public boolean equals(Object obj) {
if (obj == this) return true;
if (obj == null || obj.getClass() != getClass()) return false;
return ((Key) obj).value == value;
}
@Override
public String toString() {
return "v(" + value + ")";
}
}我们执行如下代码:
@Test
public void test03() {
HashMap<Key, Integer> map = new HashMap<>();
for (int i = 1; i < 19; i++) {
map.put(new Key(i),i);
}
System.out.println(map.get(new Key(12))); // null
}我们看一下第一个桶上面的红黑树:
┌─Node{key=v(11), value=11}─┐
│ │
┌─Node{key=v(10), value=10} ┌─Node{key=v(12), value=12}─┐
│ │ │
Node{key=v(17), value=17} ┌─Node{key=v(14), value=14} ┌─Node{key=v(16), value=16}─┐
│ │ │
Node{key=v(15), value=15} Node{key=v(13), value=13} Node{key=v(18), value=18}问题就出在,当我们从根结点往下找时,显然比较的对象的内存地址,也就是说我们不确定我们会找左子树还是右子树,如果找错就永远也找不到我们想要找的结点了
我们来测试一下看会不会有问题
@Test
public void test03() {
HashMap<Key, Integer> map = new HashMap<>();
for (int i = 1; i < 19; i++) {
map.put(new Key(i),i);
}
for (int i = 0; i < 20; i++) {
System.out.println(map.get(new Key(1)));
}
}
// 结果输出有1也有null解决方案,通过遍历确定结点应该存放的位置:
先修改我们通过key找到node结点的代码
核心代码就是如果不能通过hashCode和equals确定走向并找到,就扫描整棵红黑树进行寻找
/**
* 通过key找到node结点
*/
private Node<K, V> node(Node<K, V> node, K k1) {
// 先计算hash值
int h1 = k1 == null ? 0 : k1.hashCode();
// 存放查找的结果
Node<K, V> result = null;
while (node != null) {
K k2 = node.key;
int h2 = node.hashCode;
// 先比较hash值
if (h1 > h2) {
node = node.right;
} else if (h1 < h2) {
node = node.left;
} else if (Objects.equals(k1, k2)) {
return node;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable) {
int cmp = ((Comparable) k1).compareTo(k2);
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
}
return node;
} else if (node.right != null && (result = node(node.right, k1)) != null) {
// 哈希值相等,不具备可比较性
return result;
} else if (node.left != null && (result = node(node.left, k1)) != null) {
// 哈希值相等,不具备可比较性
return result;
}
// 遍历完了都找不到,直接返回null
return null;
}
return null;
}修改put方法
核心和上面一样,如果不能通过比较确定要往红黑树的那个分叉进行寻找的话,再通过内存地址作差计算走向,这里有一个小细节,就是hashCode不能相减,因为可以hashCode可能为负数,正数减负数就可能超出int的限制,所以我们应该直接进行比较
@Override
public V put(K key, V value) {
// 拿到索引
int index = index(key);
// 取出index位置上的红黑树结点
Node<K, V> rootNode = table[index];
if (rootNode == null) {
// 如果根结点为空,初始化结点
rootNode = new Node<>(key, value, null);
// 放到对应桶里面
table[index] = rootNode;
size++;
// 新增加了一个结点后一定要修复红黑树性质
afterPut(rootNode);
}
// 桶上面已经有结点了,即发生了hash冲突
Node<K, V> parent = rootNode;
Node<K, V> node = rootNode;
// 用来记录比较结果
int cmp = 0;
K k1 = key;
// 计算添加结点key的hash值
int h1 = key == null ? 0 : key.hashCode();
// 定义一个中间变量
Node<K, V> result = null;
do {
parent = node;
K k2 = node.key;
int h2 = node.hashCode;
// 比较hashCode
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (Objects.equals(k1, k2)) { // 通过equals方法比较
cmp = 0;
} else if (k1 != null && k2 != null // 比较类名或者自身的compareTo方法
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable) {
cmp = ((Comparable) k1).compareTo(k2);
} else { // 先进行扫描,看有没有已经存在这个结点了,然后再根据内存地址大小决定左右
if ((node.left != null && (result = node(node.left, k1)) != null)
|| (node.right != null && (result = node(node.right, k1)) != null)) {
// 表示已经存在这个key
node = result;
cmp = 0;
} else { // 不存在这个key,只能根据内存地址进行比较了
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
}
}
/*----------------------------下面是红黑树结点的摆放---------------------------------*/
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
// 相等的话覆盖
V oldValue = node.value;
node.key = key;
node.value = value;
return oldValue;
}
} while (node != null);
//添加元素
Node<K, V> newNode = new Node<>(key, value, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
//判断是否需要平衡这棵二叉树
afterPut(newNode);
return null;
}我们去测试一下,发现能够找到我们想要的结点了
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 但是我们上面put方法其实还是有一些问题的,就是每次hash冲突的时候都会对左右子树进行大量重复的扫描,例如第一次发现左子树中没有该结点,第二次比较的时候,又会去扫描一次,其实是没有必要的,我们将这一段优化一下,用一个变量来记录一下
// 用来标记是否已经扫描过整棵树了
boolean searched = false;
do {
parent = node;
K k2 = node.key;
int h2 = node.hashCode;
// 比较hashCode
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (Objects.equals(k1, k2)) { // 通过equals方法比较
cmp = 0;
} else if (k1 != null && k2 != null // 比较类名或者自身的compareTo方法
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable) {
cmp = ((Comparable) k1).compareTo(k2);
} else if (searcheded) {
// 之前已经扫描过了,发现没有该结点,直接比较内存地址即可
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
} else {
// 扫描整棵红黑树,看该结点是否已经出现过了
if ((node.left != null && (result = node(node.left, k1)) != null)
|| (node.right != null && (result = node(node.right, k1)) != null)) {
// 表示已经存在这个key
node = result;
cmp = 0;
} else {
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
// 标记已经整棵树扫描过了
searcheded = true;
}
}package com.fx.Map;
import com.fx.IMap.Map;
import com.fx.printer.BinaryTreeInfo;
import com.fx.printer.BinaryTrees;
import java.util.LinkedList;
import java.util.Objects;
import java.util.Queue;
import java.util.concurrent.atomic.AtomicBoolean;
import java.util.function.BiConsumer;
/**
* <p>
* hashmap源码学习
* </p>
*
* @since: 2022/7/15 14:57
* @author: 梁峰源
*/
@SuppressWarnings("unchecked")
public class HashMap<K, V> implements Map<K, V> {
private static final boolean RED = false;
private static final boolean BLACK = true;
/**
* size表示现在有多少个桶里面有结点了,这里要和数组长度区分开来
*/
private int size;
/**
* 数组默认的大小,必须是2的幂,1 << 4可以更方便看出幂关系
*/
private static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
/**
* 基于红黑树根结点的数组,每一个桶的位置都是一个红黑树根结点
*/
private Node<K, V>[] table;
/**
* 初始化
*/
public HashMap() {
table = new Node[DEFAULT_INITIAL_CAPACITY];
}
/**
* 红黑树结点
*
* @param <K>
* @param <V>
*/
private static class Node<K, V> {
K key;
V value;
int hashCode;
boolean color = RED;
public Node<K, V> left;//左结点
public Node<K, V> right;//右结点
public Node<K, V> parent;//父结点
public Node(K key, V value, Node<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
this.hashCode = key == null ? 0 : key.hashCode();
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
public boolean isRightChild() {
return parent != null && this == parent.right;
}
// 返回当前结点的兄弟结点
public Node<K, V> sibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
//没有兄弟结点
return null;
}
@Override
public String toString() {
return "Node{" +
"key=" + key +
", value=" + value +
'}';
}
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
if (table != null && size > 0) {
size = 0;
// 遍历每个桶,将头结点置空
for (int i = 0; i < table.length; ++i)
table[i] = null;
}
}
/**
* 计算Key的索引
*/
private int index(K key) {
// HashMap运行key为空,为空我们将其放到数组下标为0的位置
if (key == null) return 0;
// 计算hashCode
int hashCode = key.hashCode();
// 拿高16位和低16位进行混淆运算,让hash值更加离散,减少hash冲突
hashCode = hashCode ^ (hashCode >>> 16);
return hashCode & (table.length - 1);
}
@Override
public V put(K key, V value) {
// 拿到索引
int index = index(key);
// 取出index位置上的红黑树结点
Node<K, V> rootNode = table[index];
if (rootNode == null) {
// 如果根结点为空,初始化结点
rootNode = new Node<>(key, value, null);
// 放到对应桶里面
table[index] = rootNode;
size++;
// 新增加了一个结点后一定要修复红黑树性质
afterPut(rootNode);
}
// 桶上面已经有结点了,即发生了hash冲突
Node<K, V> parent = rootNode;
Node<K, V> node = rootNode;
int cmp = 0;
K k1 = key;
// 计算添加结点key的hash值
int h1 = key == null ? 0 : key.hashCode();
// 定义一个中间变量
Node<K, V> result = null;
// 用来标记是否已经扫描过整棵树了
boolean searched = false;
do {
parent = node;
K k2 = node.key;
int h2 = node.hashCode;
// 比较hashCode
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (Objects.equals(k1, k2)) { // 通过equals方法比较
cmp = 0;
} else if (k1 != null && k2 != null // 比较类名或者自身的compareTo方法
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable) {
cmp = ((Comparable) k1).compareTo(k2);
} else if (searched) {
// 之前已经扫描过了,发现没有该结点,直接比较内存地址即可
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
} else {
// 扫描整棵红黑树,看该结点是否已经出现过了
if ((node.left != null && (result = node(node.left, k1)) != null)
|| (node.right != null && (result = node(node.right, k1)) != null)) {
// 表示已经存在这个key
node = result;
cmp = 0;
} else {
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
// 标记已经整棵树扫描过了
searched = true;
}
}
/*----------------------------下面是红黑树结点的摆放---------------------------------*/
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
// 相等的话覆盖
V oldValue = node.value;
node.key = key;
node.value = value;
return oldValue;
}
} while (node != null);
//添加元素
Node<K, V> newNode = new Node<>(key, value, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
//判断是否需要平衡这棵二叉树
afterPut(newNode);
return null;
}
/**
* 通过key找到node结点
*/
private Node<K, V> node(K key) {
// 先计算hash值
Node<K, V> root = table[index(key)];
return root == null ? null : node(root, key);
}
/**
* 通过key找到node结点
*/
private Node<K, V> node(Node<K, V> node, K k1) {
// 先计算hash值
int h1 = k1 == null ? 0 : k1.hashCode();
// 存放查找的结果
Node<K, V> result = null;
int cmp = 0;
while (node != null) {
K k2 = node.key;
int h2 = node.hashCode;
// 先比较hash值
if (h1 > h2) {
node = node.right;
} else if (h1 < h2) {
node = node.left;
} else if (Objects.equals(k1, k2)) {
return node;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable
&& (cmp = ((Comparable) k1).compareTo(k2)) != 0) {
node = cmp > 0 ? node.right : node.left;
} else if (node.right != null && (result = node(node.right, k1)) != null) {
// 遍历右子树
return result;
} else {
// 只能往左边走
node = node.left;
}
}
return null;
}
@Override
public V get(K key) {
Node<K, V> node = node(key);
return node == null ? null : node.value;
}
/**
* 对外暴露的删除方法
*/
@Override
public V remove(K key) {
return remove(node(key));
}
/**
* 根据结点删除该结点
*/
private V remove(Node<K, V> node) {
if (node == null) return null;
// 计算桶的位置
int index = index(node.key);
V oldValue = node.value;
//优先处理度为2的结点
if (node.hasTwoChildren()) {
//找到其后继结点
Node<K, V> successor = successor(node);
//用后继结点的值覆盖度为2的结点的值
node.key = successor.key;
node.value = successor.value;
//因为度为2的结点的后继或者前驱结点一定是度为1或0,所以将删除结点交给后面的代码来做
node = successor;
}
//删除度为1或者度为0的结点
Node<K, V> replaceNode = node.left != null ? node.left : node.right;
/*
* 这里有三种情况,需要分类讨论
* 1. node是度为1的结点
* 2. node是叶子结点并且是根结点
* 3. node是叶子结点
*/
if (replaceNode != null) {
//先修改node.parent的指向
replaceNode.parent = node.parent;
//修改parent的left、right指向
if (node.parent == null) { //node是度为1的结点且是根结点
// 这里要替换成对应桶的位置
table[index] = replaceNode;
} else if (node == node.parent.left) {
node.parent.left = replaceNode;
} else {
node.parent.right = replaceNode;
}
//删除结点之后的处理
afterRemove(replaceNode);
} else if (node.parent == null) {
//node是叶子结点并且是根结点,直接让该结点为null
table[index] = null;
} else {
//叶子结点
//父结点的左子树
if (node == node.parent.left) {
node.parent.left = null;
} else {
//父结点右子树
node.parent.right = null;
}
//删除结点之后的处理,这里也不需要替代
afterRemove(node);
}
size--;
return oldValue;
}
/**
* 删除之后的补偿策略
*/
protected void afterRemove(Node<K, V> node) {
// 如果删除的节点是红色
// 或者 用以取代删除节点的子节点是红色
if (isRed(node)) {
black(node);
return;
}
Node<K, V> parent = node.parent;
// 删除的是黑色叶子节点【下溢】
// 判断被删除的node是左还是右
boolean left = parent.left == null || node.isLeftChild();
Node<K, V> sibling = left ? parent.right : parent.left;
if (left) { // 被删除的节点在左边,兄弟节点在右边
if (isRed(sibling)) { // 兄弟节点是红色
black(sibling);
red(parent);
rotateLeft(parent);
// 更换兄弟
sibling = parent.right;
}
// 兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// 兄弟节点没有1个红色子节点,父节点要向下跟兄弟节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent);
}
} else { // 兄弟节点至少有1个红色子节点,向兄弟节点借元素
// 兄弟节点的左边是黑色,兄弟要先旋转
if (isBlack(sibling.right)) {
rotateRight(sibling);
sibling = parent.right;
}
color(sibling, colorOf(parent));
black(sibling.right);
black(parent);
rotateLeft(parent);
}
} else { // 被删除的节点在右边,兄弟节点在左边
if (isRed(sibling)) { // 兄弟节点是红色
black(sibling);
red(parent);
rotateRight(parent);
// 更换兄弟
sibling = parent.left;
}
// 兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// 兄弟节点没有1个红色子节点,父节点要向下跟兄弟节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent);
}
} else { // 兄弟节点至少有1个红色子节点,向兄弟节点借元素
// 兄弟节点的左边是黑色,兄弟要先旋转
if (isBlack(sibling.left)) {
rotateLeft(sibling);
sibling = parent.left;
}
color(sibling, colorOf(parent));
black(sibling.left);
black(parent);
rotateRight(parent);
}
}
}
@Override
public boolean containsKey(K key) {
return node(key) != null;
}
@Override
public boolean containsValue(V value) {
// 层序遍历每个桶上面的红黑树
if (size == 0) return false;
AtomicBoolean result = new AtomicBoolean(false);
// 遍历集合
forEach((k, v) -> {
if (Objects.equals(v, value))
result.set(true);
});
return result.get();
}
@Override
public void traversal(Visitor<K, V> visitor) {
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
if (visitor.stop) return;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty() && !visitor.stop) {
// 出栈
Node<K, V> popNode = queue.poll();
// 执行回调函数
visitor.visit(popNode.key, popNode.value);
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
}
}
}
/**
* 通过forEach遍历函数
*/
@Override
public void forEach(BiConsumer<? super K, ? super V> action) {
if (action == null)
throw new NullPointerException();
// 这里手动遍历所有的桶
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty()) {
// 出栈
Node<K, V> popNode = queue.poll();
// 执行回调函数
action.accept(popNode.key, popNode.value);
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
}
}
}
/**
* 打印所有的红黑树
*/
public void showTree() {
for (int i = 0; i < table.length; i++) {
Node<K, V> node = table[i];
if (node == null) continue;
System.out.println("-----------第【" + i + "】个结点------------");
BinaryTrees.println(new BinaryTreeInfo() {
@Override
public Object root() {
return node;
}
@Override
public Object left(Object node) {
return ((Node<K, V>) node).left;
}
@Override
public Object right(Object node) {
return ((Node<K, V>) node).right;
}
@Override
public Object string(Object node) {
return node;
}
});
System.out.println("---------------------------------------");
}
}
/*--------------HashMap中的key的比较--------------*/
/**
* 规定传入对象的比较规则
*
* @param k1 第一个对象
* @param k2 第二个对象
* @param h1 k1的hash值
* @param h2 k2的hash值
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
private int compare(K k1, K k2, int h1, int h2) {
// 先比较hash值,如果hash值不同,返回hash值的差
int result = h1 - h2;
if (result != 0) return result;
// hash值一样,需要比较equals
if (Objects.equals(k1, k2)) return 0;
// hash值相等,但不equals,我们比较类名
if (k1 != null && k2 != null) {
String k1ClassName = k1.getClass().getName();
String k2ClassName = k2.getClass().getName();
// 通过类名进行比较
result = k1ClassName.compareTo(k2ClassName);
if (result != 0) return result;
// 类名也相等,继续比较,如果key实现了Comparable接口,直接进行比较
if (k1 instanceof Comparable) return ((Comparable) k1).compareTo(k2);
}
/*
* 同一种类型,但是不具备可比较性
* 1. k1为null但k2不为null
* 2. k2不为null但是k1为空
* 注意:k1、k2都为空的情况已经被上面的Objects.equals方法拦截
*/
// 到了这里,只能比较内存地址了
return System.identityHashCode(k1) - System.identityHashCode(k2);
}
/*------------------修复红黑树性质---------------------*/
/**
* 修复红黑树性质
*/
private void afterPut(Node<K, V> node) {
// 先取出父结点
Node<K, V> parent = node.parent;
// 添加的是根结点(将其染成黑色并返回)或者上溢到根结点
if (parent == null) {
black(node);
return;
}
// 如果是前四种情况,即父结点为黑色结点,不用处理
if (isBlack(parent)) return;
// 取出uncle结点
// 取出祖父结点
Node<K, V> grand = parent.parent;
Node<K, V> uncle = parent.sibling();
// 如果叔父结点是红色【B树结点上溢,只需要染色】
if (isRed(uncle)) {
black(parent);
black(uncle);
// 把祖父结点当做是新添加的结点
// 递归调用
afterPut(red(grand));
return;
}
/*
* 叔父结点不是红色,有四种情况
* LL/RR: parent染成BLACK,grand染成RED - grand进行单旋操作
* LR/RL: 自己染成black,grand染成red,再双旋
*/
if (parent.isLeftChild()) { // L
red(grand);
if (node.isLeftChild()) { // LL
black(parent);
} else { // LR
black(node);
rotateLeft(parent);
}
rotateRight(grand);
} else { //R
red(grand);
if (node.isLeftChild()) { // RL
black(node);
rotateRight(parent);
} else { // RR
black(parent);
}
rotateLeft(grand);
}
}
/**
* 对该元素进行左旋转
*
* @param grand 待旋转的结点
*/
protected void rotateLeft(Node<K, V> grand) {
if (null == grand) return;
//获得parent结点
Node<K, V> parent = grand.right;
//将parent的左子结点取出
Node<K, V> leftChild = parent.left;
//左旋
grand.right = leftChild;
parent.left = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, leftChild);
}
/**
* 对该元素进行右旋转
*
* @param grand 待旋转的结点
*/
protected void rotateRight(Node<K, V> grand) {
//获得parent结点,即grand结点的左结点
Node<K, V> parent = grand.left;
//获得parent结点的右子结点,方便后面更新高度
Node<K, V> rightChild = parent.right;
//右旋
grand.left = rightChild;
parent.right = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, rightChild);
}
/**
* 旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
*/
protected void afterRotate(Node<K, V> grand, Node<K, V> parent, Node<K, V> child) {
/*
* 让parent结点成为当前子树的根结点
* 这里有两步:
* 1. 让parent的父结点指向grand的父结点
* 2. 让grand父结点本来指向grand的指针指向parent,这里顺便更新了parent结点的父结点
**/
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else {
//当前结点没有父结点,即grand结点就是root结点
table[index(grand.key)] = parent;
}
/*
* 一共需要更新三个结点的parent,grand、parent和leftChild结点
* grand结点在上面第二步中已经更新了,所以这里我们还需要更新parent结点和leftChild结点的parent结点
**/
if (child != null) {
child.parent = grand;
}
//更新grand的parent结点
grand.parent = parent;
}
/**
* 找到当前结点的前驱结点
*/
protected Node<K, V> predecessor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
//前驱结点在左子树当中(left.right.right.......)
Node<K, V> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
/*
* 这里有两种情况
* 1. node.parent == null
* 2. node = node.parent.right;
*/
return node.parent;
}
/**
* 找到其后继结点
*/
protected Node<K, V> successor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
Node<K, V> p = node.right;
//第一种情况,其后继结点为node.right.left.left...
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
/*
* 来到这里有两种情况
* 1. node.right = null
* 2. node = node.parent.left;
*/
return node.parent;
}
//染成红色
private Node<K, V> red(Node<K, V> node) {
return color(node, RED);
}
//染成黑色
private Node<K, V> black(Node<K, V> node) {
return color(node, BLACK);
}
/**
* 将元素染色
*
* @param node 带染色的结点
* @param color 需要染的颜色
* @return 将染色的结点返回
*/
private Node<K, V> color(Node<K, V> node, boolean color) {
if (node == null) return node;
node.color = color;
return node;
}
//查看当前结点颜色
private boolean colorOf(Node<K, V> node) {
return node == null ? BLACK : node.color;
}
private boolean isBlack(Node<K, V> node) {
return colorOf(node) == BLACK;
}
private boolean isRed(Node<K, V> node) {
return colorOf(node) == RED;
}
}我们来看一下Java HashMap的put方法
再看一下比较的过程,看来写的和我们差不多😜😜😜
我们可以看到,其实当一个桶上面的结点数量过多时,其实从红黑树上面找到一个结点,过程还是很复杂的,如果一个桶上面红黑树高度高达上万的高度,那性能一定会下降的很厉害,所以我们自然而然的想到
如果红黑树过高,我们就将桶的数量增大,将红黑树分一些高度给其他的桶
但是到底红黑树高度达到多少时需要进行扩容呢?我们来看一个概念
装填因子(Load Factor):节点总数量 / 哈希表桶数组长度,也叫做负载因子
在JDK1.8的HashMap中,如果装填因子超过0.75,就扩容为原来的2倍
我们来看一下我们的数据如何进行移动,首先我们要有一个方法,判断当装填因子超过了这个值的时候,就好进行扩容
/**
* 判断是否需要对数组容量进行扩容
*/
private void resize() {
// 装填因子小于等于0.75
if(size / table.length <= DEFAULT_LOAD_FACTOR) return;
// 先保留一下旧的数组
Node<K,V>[] oldTable = table;
// 扩容两倍
table = new Node[oldTable.length << 1];
// 扩容后的操作
}现在的问题就是扩容后如何将原来桶上面的数据分到新的桶上面,有一种做法是采用拷贝的方式,类似于
// 这里手动遍历所有的桶
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty()) {
// 出栈
Node<K, V> popNode = queue.poll();
// 这里将所有的数据复制到新的数组位置
Node<K,V> node = queue.poll();
put(node.key,node.value);
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
}
}但是显然这种方式是不可取的,这样会将原本有的数据再重新拷贝一份,那我们如何处理呢?应该拿到将这棵红黑树直接移动到新的桶上面去吗?显然不可能,因为所有的结点所在桶的位置都可能会发生改变
hash(key) & (table.length - 1)我们来演示一下这个过程
// 假设一开始容量是 2^2,key的hashCode为1110,可以算出索引为10
1110
& 11
10
// 如果现在扩容为 2^3
1110
& 111
110
// 还有一种情况是没有变化的
1010
& 111
010 显然对应桶上面红黑树结点的HashCode再扩容之后其实可能会发生改变,所以扩容之后有两种情况
- 索引没有发生改变
- 索引高位多了一个1
其实取决于旧hashCode对应的那一位,如果为0,则不影响;如果是1,索引高位多了一个1
那么二进制高位加一在十进制里面是如何体现的呢?其实就是十进制加上了就数组的长度
// 以上面的栗子为例
10 -> 110
其实就是加了 100 -> 加了4 -> 加了2^2 -> 加了旧数组的长度即当我扩容时,有两种情况:
- 索引没有发生改变
- 索引为旧索引加上旧数组长度(index = index + table.length)
这里就可以接上上面埋下的伏笔了,为什么计算桶位置的时候要
& (table.length - 1),而不是直接取模,其实是为了在数组扩容移动结点的时候,能够通过index = index + table.length直接拿到新的索引位置,而不是再去计算一次hash值,如果再去计算一次hash,每个结点的hash值都可能不一样,但是这里我们就只有两种情况,且有很大一部分的结点根本就不需要移动桶的位置
现在我们要做的就是将桶上面红黑树中每个结点重新计算hash,再移动到新的桶上面
/**
* 判断是否需要对数组容量进行扩容
*/
private void resize() {
// 装填因子小于等于0.75
if(size / table.length <= DEFAULT_LOAD_FACTOR) return;
// 先保留一下旧的数组
Node<K,V>[] oldTable = table;
// 扩容两倍
table = new Node[oldTable.length << 1];
// 移动所有的结点到新的桶上面
// 这里手动遍历所有的桶
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : oldTable) {
if (kvNode == null) continue;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty()) {
// 出栈
Node<K, V> popNode = queue.poll();
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
// 挪动结点,需要写在入队代码之后
moveNode(kvNode);
}
}
}
private int index(Node<K, V> node) {
return node.hashCode & (table.length - 1);
}
private void moveNode(Node<K,V> newNode){
// 重置该结点的所有引用
newNode.parent = null;
newNode.left = null;
newNode.right = null;
// 树结点默认应该为red
red(newNode);
// 拿到索引
int index = index(newNode);
// 取出index位置上的红黑树结点
Node<K, V> rootNode = table[index];
if (rootNode == null) {
// 如果根结点为空,初始化结点
rootNode = newNode;
// 放到对应桶里面
table[index] = rootNode;
// 新增加了一个结点后一定要修复红黑树性质
afterPut(rootNode);
return;
}
// 桶上面已经有结点了,即发生了hash冲突
Node<K, V> parent;
Node<K, V> node = rootNode;
int cmp = 0;
K key = newNode.key;
// 计算添加结点key的hash值
int h1 = newNode.hashCode;
do {
K k2 = node.key;
int h2 = node.hashCode;
// 挪动的时候只需要考虑是往左走还是往右走,不需要equals
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (key != null && k2 != null // 比较类名或者自身的compareTo方法
&& key.getClass() == k2.getClass()
&& key instanceof Comparable
&& (cmp = ((Comparable) key).compareTo(k2)) != 0) {
// nothing to do
} else {
cmp = System.identityHashCode(key) - System.identityHashCode(k2);
}
/*----------------------------下面是红黑树结点的摆放---------------------------------*/
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
}
} while (node != null);
// 因为是移动结点,不可能出现相等的情况
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
// 设置移动结点的父结点
newNode.parent = parent;
//判断是否需要平衡这棵二叉树
afterPut(newNode);
}我们来测试一下,对于HashMap扩容带来的性能提升
测试代码,添加一千万的元素
@Test
public void test06() {
LocalDateTime start = LocalDateTime.now();
Map<Integer,Integer> map = new HashMap<>();
for (int i = 0; i < 10_000_000; i++) {
map.put(i,i);
}
System.out.println(map.size());
System.out.println("添加元素耗时:" + Duration.between(start,LocalDateTime.now()).toMillis() + "ms");
}不扩容:
存储元素个数为:10000000
添加元素耗时:8747ms扩容:
map进行了扩容,原容量为:16,新容量为:32
map进行了扩容,原容量为:32,新容量为:64
map进行了扩容,原容量为:64,新容量为:128
map进行了扩容,原容量为:128,新容量为:256
map进行了扩容,原容量为:256,新容量为:512
map进行了扩容,原容量为:512,新容量为:1024
map进行了扩容,原容量为:1024,新容量为:2048
map进行了扩容,原容量为:2048,新容量为:4096
map进行了扩容,原容量为:4096,新容量为:8192
map进行了扩容,原容量为:8192,新容量为:16384
map进行了扩容,原容量为:16384,新容量为:32768
map进行了扩容,原容量为:32768,新容量为:65536
map进行了扩容,原容量为:65536,新容量为:131072
map进行了扩容,原容量为:131072,新容量为:262144
map进行了扩容,原容量为:262144,新容量为:524288
map进行了扩容,原容量为:524288,新容量为:1048576
map进行了扩容,原容量为:1048576,新容量为:2097152
map进行了扩容,原容量为:2097152,新容量为:4194304
map进行了扩容,原容量为:4194304,新容量为:8388608
map进行了扩容,原容量为:8388608,新容量为:16777216
存储元素个数为:10000000
添加元素耗时:8551ms我们来看一下查询的效率:
@Test
public void test06() {
LocalDateTime start = LocalDateTime.now();
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < 10_000_000; i++) {
map.put(i, i);
}
System.out.println("存储元素个数为:" + map.size());
System.out.println("耗时:" + Duration.between(start, LocalDateTime.now()).toMillis() + "ms");
start = LocalDateTime.now();
for (int i = 0; i < 1_000_000; i++) {
map.get(i);
}
System.out.println("查询一百万条数据耗时:" + Duration.between(start, LocalDateTime.now()).toMillis() + "ms");
}存储元素个数为:10000000
存储元素耗时:8223ms
查询一百万条数据耗时:95msmap进行了扩容,原容量为:16,新容量为:32
map进行了扩容,原容量为:32,新容量为:64
map进行了扩容,原容量为:64,新容量为:128
map进行了扩容,原容量为:128,新容量为:256
map进行了扩容,原容量为:256,新容量为:512
map进行了扩容,原容量为:512,新容量为:1024
map进行了扩容,原容量为:1024,新容量为:2048
map进行了扩容,原容量为:2048,新容量为:4096
map进行了扩容,原容量为:4096,新容量为:8192
map进行了扩容,原容量为:8192,新容量为:16384
map进行了扩容,原容量为:16384,新容量为:32768
map进行了扩容,原容量为:32768,新容量为:65536
map进行了扩容,原容量为:65536,新容量为:131072
map进行了扩容,原容量为:131072,新容量为:262144
map进行了扩容,原容量为:262144,新容量为:524288
map进行了扩容,原容量为:524288,新容量为:1048576
map进行了扩容,原容量为:1048576,新容量为:2097152
map进行了扩容,原容量为:2097152,新容量为:4194304
map进行了扩容,原容量为:4194304,新容量为:8388608
map进行了扩容,原容量为:8388608,新容量为:16777216
存储元素个数为:10000000
存储元素耗时:6985ms
查询一百万条数据耗时:26ms可以看出HashMap在进行扩容后,查询效率大大提升!
其实写完了HashMap之后再去看JDK的HashMap源码,会有一种豁然开朗的感觉
参考博客:史上最详细的 JDK 1.8 HashMap 源码解析
package com.fx.Map;
import com.fx.IMap.Map;
import com.fx.printer.BinaryTreeInfo;
import com.fx.printer.BinaryTrees;
import java.util.LinkedList;
import java.util.Objects;
import java.util.Queue;
import java.util.concurrent.atomic.AtomicBoolean;
import java.util.function.BiConsumer;
/**
* <p>
* hashmap源码学习
* </p>
*
* @since: 2022/7/15 14:57
* @author: 梁峰源
*/
@SuppressWarnings("unchecked")
public class HashMap<K, V> implements Map<K, V> {
private static final boolean RED = false;
private static final boolean BLACK = true;
/**
* size表示现在有多少个桶里面有结点了,这里要和数组长度区分开来
*/
private int size;
/**
* 数组默认的大小,必须是2的幂,1 << 4可以更方便看出幂关系
*/
private static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
/**
* 装填因子,等于节点总数量 / 哈希表桶数组长度
*/
private static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* 基于红黑树根结点的数组,每一个桶的位置都是一个红黑树根结点
*/
private Node<K, V>[] table;
/**
* 初始化
*/
public HashMap() {
table = new Node[DEFAULT_INITIAL_CAPACITY];
}
/**
* 红黑树结点
*
* @param <K>
* @param <V>
*/
private static class Node<K, V> {
K key;
V value;
int hashCode;
boolean color = RED;
public Node<K, V> left;//左结点
public Node<K, V> right;//右结点
public Node<K, V> parent;//父结点
public Node(K key, V value, Node<K, V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
this.hashCode = key == null ? 0 : key.hashCode();
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
public boolean isRightChild() {
return parent != null && this == parent.right;
}
// 返回当前结点的兄弟结点
public Node<K, V> sibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
//没有兄弟结点
return null;
}
@Override
public String toString() {
return "Node{" +
"key=" + key +
", value=" + value +
'}';
}
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
if (table != null && size > 0) {
size = 0;
// 遍历每个桶,将头结点置空
for (int i = 0; i < table.length; ++i)
table[i] = null;
}
}
/**
* 计算Key的索引
*/
private int index(K key) {
return hash(key) & (table.length - 1);
}
/**
* 对key进行扰动计算
*/
private int hash(K key) {
// HashMap运行key为空,为空我们将其放到数组下标为0的位置
if (key == null) return 0;
// 计算hashCode
int hashCode = key.hashCode();
// 拿高16位和低16位进行混淆运算,让hash值更加离散,减少hash冲突
hashCode = hashCode ^ (hashCode >>> 16);
return hashCode;
}
private int index(Node<K, V> node) {
return node.hashCode & (table.length - 1);
}
@Override
public V put(K key, V value) {
// 检测是否需要扩容
resize();
// 拿到索引
int index = index(key);
// 取出index位置上的红黑树结点
Node<K, V> rootNode = table[index];
if (rootNode == null) {
// 如果根结点为空,初始化结点
rootNode = new Node<>(key, value, null);
// 放到对应桶里面
table[index] = rootNode;
size++;
// 新增加了一个结点后一定要修复红黑树性质
afterPut(rootNode);
return value;
}
// 桶上面已经有结点了,即发生了hash冲突
Node<K, V> parent;
Node<K, V> node = rootNode;
int cmp = 0;
// 计算添加结点key的hash值
int h1 = hash(key);
// 定义一个中间变量
Node<K, V> result = null;
// 用来标记是否已经扫描过整棵树了
boolean searched = false;
do {
parent = node;
K k2 = node.key;
int h2 = node.hashCode;
// 比较hashCode
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (Objects.equals(key, k2)) { // 通过equals方法比较
cmp = 0;
} else if (key != null && k2 != null // 比较类名或者自身的compareTo方法
&& key.getClass() == k2.getClass()
&& key instanceof Comparable
&& (cmp = ((Comparable) key).compareTo(k2)) != 0) {
// nothing to do
} else if (searched) {
// 之前已经扫描过了,发现没有该结点,直接比较内存地址即可
cmp = System.identityHashCode(key) - System.identityHashCode(k2);
} else {
// 扫描整棵红黑树,看该结点是否已经出现过了
if ((node.left != null && (result = node(node.left, key)) != null)
|| (node.right != null && (result = node(node.right, key)) != null)) {
// 表示已经存在这个key
node = result;
cmp = 0;
} else {
cmp = System.identityHashCode(key) - System.identityHashCode(k2);
// 标记已经整棵树扫描过了
searched = true;
}
}
/*----------------------------下面是红黑树结点的摆放---------------------------------*/
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
// 相等的话覆盖
V oldValue = node.value;
node.key = key;
node.value = value;
return oldValue;
}
} while (node != null);
//添加元素
Node<K, V> newNode = new Node<>(key, value, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
//判断是否需要平衡这棵二叉树
afterPut(newNode);
return null;
}
/**
* 判断是否需要对数组容量进行扩容
*/
private void resize() {
// 装填因子小于等于0.75
if(size / table.length <= DEFAULT_LOAD_FACTOR) return;
System.out.println("map进行了扩容,原容量为:" + table.length +",新容量为:" + (table.length << 1));
// 先保留一下旧的数组
Node<K,V>[] oldTable = table;
// 扩容两倍
table = new Node[oldTable.length << 1];
// 移动所有的结点到新的桶上面
// 这里手动遍历所有的桶
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : oldTable) {
if (kvNode == null) continue;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty()) {
// 出栈
Node<K, V> popNode = queue.poll();
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
// 挪动结点,需要写在入队代码之后
moveNode(kvNode);
}
}
}
private void moveNode(Node<K,V> newNode){
// 重置该结点的所有引用
newNode.parent = null;
newNode.left = null;
newNode.right = null;
// 树结点默认应该为red
red(newNode);
// 拿到索引
int index = index(newNode);
// 取出index位置上的红黑树结点
Node<K, V> rootNode = table[index];
if (rootNode == null) {
// 如果根结点为空,初始化结点
rootNode = newNode;
// 放到对应桶里面
table[index] = rootNode;
// 新增加了一个结点后一定要修复红黑树性质
afterPut(rootNode);
return;
}
// 桶上面已经有结点了,即发生了hash冲突
Node<K, V> parent;
Node<K, V> node = rootNode;
int cmp = 0;
K key = newNode.key;
// 计算添加结点key的hash值
int h1 = newNode.hashCode;
do {
K k2 = node.key;
int h2 = node.hashCode;
// 挪动的时候只需要考虑是往左走还是往右走,不需要equals
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (key != null && k2 != null // 比较类名或者自身的compareTo方法
&& key.getClass() == k2.getClass()
&& key instanceof Comparable
&& (cmp = ((Comparable) key).compareTo(k2)) != 0) {
// nothing to do
} else {
cmp = System.identityHashCode(key) - System.identityHashCode(k2);
}
/*----------------------------下面是红黑树结点的摆放---------------------------------*/
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
}
} while (node != null);
// 因为是移动结点,不可能出现相等的情况
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
// 设置移动结点的父结点
newNode.parent = parent;
//判断是否需要平衡这棵二叉树
afterPut(newNode);
}
/**
* 通过key找到node结点
*/
private Node<K, V> node(K key) {
// 先计算hash值
Node<K, V> root = table[index(key)];
return root == null ? null : node(root, key);
}
/**
* 通过key找到node结点
*/
private Node<K, V> node(Node<K, V> node, K k1) {
// 先计算hash值,k1需要经过扰动计算
int h1 = hash(k1);
// 存放查找的结果
Node<K, V> result = null;
int cmp = 0;
while (node != null) {
K k2 = node.key;
// h2是经过了扰动计算的
int h2 = node.hashCode;
// 先比较hash值
if (h1 > h2) {
node = node.right;
} else if (h1 < h2) {
node = node.left;
} else if (Objects.equals(k1, k2)) {
return node;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable
&& (cmp = ((Comparable) k1).compareTo(k2)) != 0) {
node = cmp > 0 ? node.right : node.left;
} else if (node.right != null && (result = node(node.right, k1)) != null) {
// 遍历右子树
return result;
} else {
// 只能往左边走
node = node.left;
}
}
return null;
}
@Override
public V get(K key) {
Node<K, V> node = node(key);
return node == null ? null : node.value;
}
/**
* 对外暴露的删除方法
*/
@Override
public V remove(K key) {
return remove(node(key));
}
/**
* 根据结点删除该结点
*/
private V remove(Node<K, V> node) {
if (node == null) return null;
// 计算桶的位置
int index = index(node.key);
V oldValue = node.value;
//优先处理度为2的结点
if (node.hasTwoChildren()) {
//找到其后继结点
Node<K, V> successor = successor(node);
//用后继结点的值覆盖度为2的结点的值
node.key = successor.key;
node.value = successor.value;
//因为度为2的结点的后继或者前驱结点一定是度为1或0,所以将删除结点交给后面的代码来做
node = successor;
}
//删除度为1或者度为0的结点
Node<K, V> replaceNode = node.left != null ? node.left : node.right;
/*
* 这里有三种情况,需要分类讨论
* 1. node是度为1的结点
* 2. node是叶子结点并且是根结点
* 3. node是叶子结点
*/
if (replaceNode != null) {
//先修改node.parent的指向
replaceNode.parent = node.parent;
//修改parent的left、right指向
if (node.parent == null) { //node是度为1的结点且是根结点
// 这里要替换成对应桶的位置
table[index] = replaceNode;
} else if (node == node.parent.left) {
node.parent.left = replaceNode;
} else {
node.parent.right = replaceNode;
}
//删除结点之后的处理
afterRemove(replaceNode);
} else if (node.parent == null) {
//node是叶子结点并且是根结点,直接让该结点为null
table[index] = null;
} else {
//叶子结点
//父结点的左子树
if (node == node.parent.left) {
node.parent.left = null;
} else {
//父结点右子树
node.parent.right = null;
}
//删除结点之后的处理,这里也不需要替代
afterRemove(node);
}
size--;
return oldValue;
}
/**
* 删除之后的补偿策略
*/
protected void afterRemove(Node<K, V> node) {
// 如果删除的节点是红色
// 或者 用以取代删除节点的子节点是红色
if (isRed(node)) {
black(node);
return;
}
Node<K, V> parent = node.parent;
// 删除的是黑色叶子节点【下溢】
// 判断被删除的node是左还是右
boolean left = parent.left == null || node.isLeftChild();
Node<K, V> sibling = left ? parent.right : parent.left;
if (left) { // 被删除的节点在左边,兄弟节点在右边
if (isRed(sibling)) { // 兄弟节点是红色
black(sibling);
red(parent);
rotateLeft(parent);
// 更换兄弟
sibling = parent.right;
}
// 兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// 兄弟节点没有1个红色子节点,父节点要向下跟兄弟节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent);
}
} else { // 兄弟节点至少有1个红色子节点,向兄弟节点借元素
// 兄弟节点的左边是黑色,兄弟要先旋转
if (isBlack(sibling.right)) {
rotateRight(sibling);
sibling = parent.right;
}
color(sibling, colorOf(parent));
black(sibling.right);
black(parent);
rotateLeft(parent);
}
} else { // 被删除的节点在右边,兄弟节点在左边
if (isRed(sibling)) { // 兄弟节点是红色
black(sibling);
red(parent);
rotateRight(parent);
// 更换兄弟
sibling = parent.left;
}
// 兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// 兄弟节点没有1个红色子节点,父节点要向下跟兄弟节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent);
}
} else { // 兄弟节点至少有1个红色子节点,向兄弟节点借元素
// 兄弟节点的左边是黑色,兄弟要先旋转
if (isBlack(sibling.left)) {
rotateLeft(sibling);
sibling = parent.left;
}
color(sibling, colorOf(parent));
black(sibling.left);
black(parent);
rotateRight(parent);
}
}
}
@Override
public boolean containsKey(K key) {
return node(key) != null;
}
@Override
public boolean containsValue(V value) {
// 层序遍历每个桶上面的红黑树
if (size == 0) return false;
AtomicBoolean result = new AtomicBoolean(false);
// 遍历集合
forEach((k, v) -> {
if (Objects.equals(v, value))
result.set(true);
});
return result.get();
}
@Override
public void traversal(Visitor<K, V> visitor) {
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
if (visitor.stop) return;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty() && !visitor.stop) {
// 出栈
Node<K, V> popNode = queue.poll();
// 执行回调函数
visitor.visit(popNode.key, popNode.value);
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
}
}
}
/**
* 通过forEach遍历函数
*/
@Override
public void forEach(BiConsumer<? super K, ? super V> action) {
if (action == null)
throw new NullPointerException();
// 这里手动遍历所有的桶
// 准备一个栈
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
// 将桶上根结点入队
queue.offer(kvNode);
while (!queue.isEmpty()) {
// 出栈
Node<K, V> popNode = queue.poll();
// 执行回调函数
action.accept(popNode.key, popNode.value);
if (popNode.left != null) queue.offer(popNode.left);
if (popNode.right != null) queue.offer(popNode.right);
}
}
}
/**
* 打印所有的红黑树
*/
public void showTree() {
for (int i = 0; i < table.length; i++) {
Node<K, V> node = table[i];
if (node == null) continue;
System.out.println("-----------第【" + i + "】个结点------------");
BinaryTrees.println(new BinaryTreeInfo() {
@Override
public Object root() {
return node;
}
@Override
public Object left(Object node) {
return ((Node<K, V>) node).left;
}
@Override
public Object right(Object node) {
return ((Node<K, V>) node).right;
}
@Override
public Object string(Object node) {
return node;
}
});
System.out.println("---------------------------------------");
}
}
/*--------------HashMap中的key的比较--------------*/
/**
* 规定传入对象的比较规则
*
* @param k1 第一个对象
* @param k2 第二个对象
* @param h1 k1的hash值
* @param h2 k2的hash值
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
private int compare(K k1, K k2, int h1, int h2) {
// 先比较hash值,如果hash值不同,返回hash值的差
int result = h1 - h2;
if (result != 0) return result;
// hash值一样,需要比较equals
if (Objects.equals(k1, k2)) return 0;
// hash值相等,但不equals,我们比较类名
if (k1 != null && k2 != null) {
String k1ClassName = k1.getClass().getName();
String k2ClassName = k2.getClass().getName();
// 通过类名进行比较
result = k1ClassName.compareTo(k2ClassName);
if (result != 0) return result;
// 类名也相等,继续比较,如果key实现了Comparable接口,直接进行比较
if (k1 instanceof Comparable) return ((Comparable) k1).compareTo(k2);
}
/*
* 同一种类型,但是不具备可比较性
* 1. k1为null但k2不为null
* 2. k2不为null但是k1为空
* 注意:k1、k2都为空的情况已经被上面的Objects.equals方法拦截
*/
// 到了这里,只能比较内存地址了
return System.identityHashCode(k1) - System.identityHashCode(k2);
}
/*------------------修复红黑树性质---------------------*/
/**
* 修复红黑树性质
*/
private void afterPut(Node<K, V> node) {
// 先取出父结点
Node<K, V> parent = node.parent;
// 添加的是根结点(将其染成黑色并返回)或者上溢到根结点
if (parent == null) {
black(node);
return;
}
// 如果是前四种情况,即父结点为黑色结点,不用处理
if (isBlack(parent)) return;
// 取出uncle结点
// 取出祖父结点
Node<K, V> grand = parent.parent;
Node<K, V> uncle = parent.sibling();
// 如果叔父结点是红色【B树结点上溢,只需要染色】
if (isRed(uncle)) {
black(parent);
black(uncle);
// 把祖父结点当做是新添加的结点
// 递归调用
afterPut(red(grand));
return;
}
/*
* 叔父结点不是红色,有四种情况
* LL/RR: parent染成BLACK,grand染成RED - grand进行单旋操作
* LR/RL: 自己染成black,grand染成red,再双旋
*/
if (parent.isLeftChild()) { // L
red(grand);
if (node.isLeftChild()) { // LL
black(parent);
} else { // LR
black(node);
rotateLeft(parent);
}
rotateRight(grand);
} else { //R
red(grand);
if (node.isLeftChild()) { // RL
black(node);
rotateRight(parent);
} else { // RR
black(parent);
}
rotateLeft(grand);
}
}
/**
* 对该元素进行左旋转
*
* @param grand 待旋转的结点
*/
protected void rotateLeft(Node<K, V> grand) {
if (null == grand) return;
//获得parent结点
Node<K, V> parent = grand.right;
//将parent的左子结点取出
Node<K, V> leftChild = parent.left;
//左旋
grand.right = leftChild;
parent.left = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, leftChild);
}
/**
* 对该元素进行右旋转
*
* @param grand 待旋转的结点
*/
protected void rotateRight(Node<K, V> grand) {
//获得parent结点,即grand结点的左结点
Node<K, V> parent = grand.left;
//获得parent结点的右子结点,方便后面更新高度
Node<K, V> rightChild = parent.right;
//右旋
grand.left = rightChild;
parent.right = grand;
//旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
afterRotate(grand, parent, rightChild);
}
/**
* 旋转之后让parent结点成为根结点并更新grand、parent、child结点的高度
*/
protected void afterRotate(Node<K, V> grand, Node<K, V> parent, Node<K, V> child) {
/*
* 让parent结点成为当前子树的根结点
* 这里有两步:
* 1. 让parent的父结点指向grand的父结点
* 2. 让grand父结点本来指向grand的指针指向parent,这里顺便更新了parent结点的父结点
**/
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else {
//当前结点没有父结点,即grand结点就是root结点
table[index(grand.key)] = parent;
}
/*
* 一共需要更新三个结点的parent,grand、parent和leftChild结点
* grand结点在上面第二步中已经更新了,所以这里我们还需要更新parent结点和leftChild结点的parent结点
**/
if (child != null) {
child.parent = grand;
}
//更新grand的parent结点
grand.parent = parent;
}
/**
* 找到当前结点的前驱结点
*/
protected Node<K, V> predecessor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
//前驱结点在左子树当中(left.right.right.......)
Node<K, V> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
/*
* 这里有两种情况
* 1. node.parent == null
* 2. node = node.parent.right;
*/
return node.parent;
}
/**
* 找到其后继结点
*/
protected Node<K, V> successor(Node<K, V> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
Node<K, V> p = node.right;
//第一种情况,其后继结点为node.right.left.left...
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
/*
* 来到这里有两种情况
* 1. node.right = null
* 2. node = node.parent.left;
*/
return node.parent;
}
//染成红色
private Node<K, V> red(Node<K, V> node) {
return color(node, RED);
}
//染成黑色
private Node<K, V> black(Node<K, V> node) {
return color(node, BLACK);
}
/**
* 将元素染色
*
* @param node 带染色的结点
* @param color 需要染的颜色
* @return 将染色的结点返回
*/
private Node<K, V> color(Node<K, V> node, boolean color) {
if (node == null) return node;
node.color = color;
return node;
}
//查看当前结点颜色
private boolean colorOf(Node<K, V> node) {
return node == null ? BLACK : node.color;
}
private boolean isBlack(Node<K, V> node) {
return colorOf(node) == BLACK;
}
private boolean isRed(Node<K, V> node) {
return colorOf(node) == RED;
}
}6.HashMap的table的容量如何确定?loadFactor是什么?该容量如何变化?这种变化会带来什么问题?
9.拉链法导致的链表过深问题为什么不用二叉查找树代替,而选择红黑树?为什么不一直使用红黑树?
在jdk1.8之前采用的是头插法,而不是尾插法,这里就有一个著名的问题:HashMap死循环问题
HashMap死循环问题其实是由HashMap自身的工作机制 + 并发操作导致的(jdk1.8解决),首先我们需要知道hashMap的底层扩容机制
当HashMap进行扩容的时候,会将原来的链表从尾结点开始重新指向,最后变为逆序指向
现在我们来还原一下案发现场,现在有两个线程t1、t2都准备对HashMap进行扩容,这两个线程指向结点的下一个结点此时都是B结点
此时假设线程T2的时间片用完了,进入休眠状态,由线程T1来完成扩容操作,当扩容完成时,线程T2的指向并没有发生改变(这里还牵涉到线程本地变量和共享变量的问题,显然此时线程T1使用的是本地变量)
此时线程T2恢复执行,继续之前的操作,准备进行头插法插入结点,但是显然此时线程结点的下一个结点为B结点,即指向B结点,这样就形成了环,但是如果是尾插法,那么T2.next会往下找,直到找到最后一个结点(即T2.next == null为止),显然不会出现死循环
抛开现象看本质,死循环问题的本事还是线程安全性问题,即使jdk1.8后没有了成环的问题,但是还是存在线程安全问题,所以在多线程的场景下我们必须使用ConcurrentHashMap