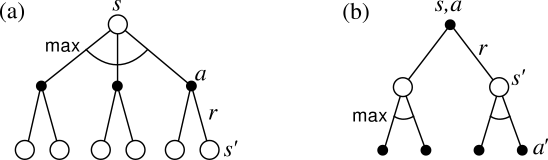Skip to content

Latest commit

 

History

History
322 lines (221 loc) · 15.1 KB

Reinforcement_Learning.md

File metadata and controls

322 lines (221 loc) · 15.1 KB
Raw

Reinforcement Learning

Overview

  • Reinforcement learning optimizs an agent for sparse, time delayed labels called rewards in an environment.

the basic idea and elements involved in a reinforcement learning model

Terms of Reinforcement Learning

  • Agent
  • Action (A)
  • Discount factor (gamma γ)
  • Environment: Physical world in which the agent operates
  • State (S): Current situation of the agent
  • Reward (R): Feedback from the environment
    • $Q_n \doteq \frac{\sum_{i=1}^{n-1} R_i}{n-1}$
    • $Q_{n+1} = Q_n + \frac{1}{n} [R_n - Q_n]$
    • $Q_{n+1} = Q_n + \alpha [R_n - Q_n] = (1 - \alpha)^n Q_1 + \sum_{i=1}^n \alpha (1 - \alpha)^{n-i} R_i$
      • $\alpha$ is a constant, step-size parameter, $0 < \alpha \leq 1$
  • Policy (π): Method to map agent’s state to actions
  • Value (V): Future reward that an agent would receive by taking an action in a particular state
  • Q-value or action-value (Q)
    • Projection of Action-Reward
      • $q^*(a) \doteq \mathbb{E}{R|A_i=a}$ The ideal (expected) reward of action $a$
      • $Q_t(a)$ The expectation reward of action $a$ at time $t$
  • Trajectory

Strategy

  • Exploration 探索法: Keep searching for new strategies
    • Probability $\epsilon$ to explore
  • Exploitation 利用法: Exploiting the best strategies found thus far
    • Probability $1 - \epsilon$ to exploit
    • $\displaystyle A^* \doteq \arg\max_a Q_t(a)$

Other Terms in RL

(Some terms using in Monte Carlo Tree Search (MCTS))

  • State Value: How good a given state is for an agent to be in. A measurement of the expected oucome (or reward) if we're in this state with respect to our final goal.
  • Playout: A simulation of the game that mimics the cause and effect of random action until reach a 'terminal' point. (reliant on a forward model that can tell us outcomes of an action of any state)

Action Selection Strategy

  • greedy
  • $\epsilon$-greedy
  • UCB (Upper Confidential Bounder)
  • Gradient

Problem Space of Reinforcement Learning

- Single State Associative Multiple State
Instructive feedback Averaging Supervised Learning -
Evaluative feedback Bandits (Function optimization) Associative Search (Contextual bandits) Markov Decision Process
  • Instructive feedback: human labeled output (which is good or bad action)
  • Evaluative feedback: the procedure don't need human involve. evaluate environment
  • MDP vs. Bandit
    • Bandit: the environment is consistent
    • MDP: your actions will change the environment(state)

Background

  • Markov Chain: The future is only related to "current state", and it has nothing to do with the past.
  • MDP Framework
    • Abstract of physical world
    • Learning by interaction of "action"

Markov Decision Processes (MDPs)

Markov Decision Process (MDP) - a mathematical framework for modeling decisions using states, actions, and rewards.

  • A Mathematical formulation of the RL problem
  • Markov property: Current state completely characterises the state of the word
  • It is a random process without memory
  • The reinforcement learning "with model"
    • (Q-learning is RL "without model")

Definitions: $(S, A, R, \mathbb{P}, \gamma)$

  • $S$: set of possible states
  • $A$: set of possible acitons
  • $R$: distribution of reward given (state, action) pair
  • $\mathbb{P}$: transition probability (i.e. distribution over next state given (state, aciton) pair)
  • $\gamma$: discount factor

Pseudo-process of MDP

  1. At time t = 0, environment samples initial states s
  2. Do until done:
    1. Agent selects action $a_t$
    2. Environment samples reward $r_t \sim R(.|s_t, a_t)$
    3. Environment samples next state $s_{t+1} \sim P(.|s_t, a_t)$
    4. Agent receives reward $r_t$ and next state $s_{t+1}$
  • Policy
    • For every state project to an action
    • Calculate a Policy such that maximize the cumulated reward
  • A policy $\pi$ is a function from $S$ to $A$ that specifies what aciton to take in each state.
  • Objective: find policy $\pi^*$ that maximizes cumulative discounted reward: $\displaystyle\sum_{t\geq 0} \gamma^t r_t$

The optimal policy $\pi^*$: Maximize the expected sum of rewards

Formally:

$$ \pi^* = \arg \max_\pi \mathbb{E} \begin{bmatrix}\displaystyle \sum_{t\geq 0} \gamma^t r_t | \pi \end{bmatrix} $$

Value function at state $s$ under a policy $pi$: the expected cumulative reward from following the policy $\pi$ from state $s$ (Represent how good is a state)

  • value function: functions of states (or of state-action pairs) that estimate how good it is for the aget to be in a give state (or how good it is to perform a given action in a given state)
  • how good: is defined in terms of future rewards that can be expected, or, to be precise, in terms of expected return

$$ V_\pi(s) = \mathbb{E} \begin{bmatrix}\displaystyle \sum_{t\geq 0} \gamma^t r_t | s_0 = s, \pi \end{bmatrix} $$

Action-value Function (Q-value function) taking action $a$ at state $s$ under policy $\pi$: the expected cumulative reward from taking aciton a in state s and then following the policy (Represent how good is a state-action pair)

a function that calculates the quality of a state-action combination

$$ Q_\pi(s, a) = \mathbb{E} \begin{bmatrix}\displaystyle \sum_{t\geq 0} \gamma^t r_t | s_0 = s, a_0 = a, \pi \end{bmatrix} $$

optimal Q-value function Q* is the maximum expected cumulative reward achievable from a given (state, aciton) paird

$$ Q^*(s, a) = \max_\pi \mathbb{E} \begin{bmatrix}\displaystyle \sum_{t\geq 0} \gamma^t r_t | s_0 = s, a_0 = a, \pi \end{bmatrix} $$

Backup diagrams for (a) $V^$ and (b) $Q^$

backup diagram

Bellman equation: expresses a relationshp between the vlaue of a state and the vlues of its sucessor states

$$ V_\pi(s) = \underbrace{\sum_a \pi(a|s)}\text{prob. of taking action $a$} \underbrace{\sum{s', r} p(s', r| s, a)}\text{prob. from $(s, a)$ to $s'$} [r + \gamma v\pi(s')] \quad \forall s \in S $$

Bellman optimality equation: expresses the fact that the value of a state under an optimal policy must equal the expected return for the best action from that state (that $Q^*$ satisfied)

$$ Q^(s, a) = \mathbb{E}{s' \sim \varepsilon} \begin{bmatrix}\displaystyle r + \gamma \max{a'} Q^(s', a') | s, a \end{bmatrix} $$

Intuiiton: if the optimal state-aciton values for the next time-stemp $Q^(s', a')$ are known, then the optimal strategy is to take the action that maximizes the expected value of $r + \gamma Q^(s', a')$

So the optimal policy $\pi^$ corresponds to taking the best action in any state as specified by $Q^$

Value Iteration Algorithm: Use Bellman equation as an iterative update

$$ Q_{i+1}(s, a) = \mathbb{E}{s' \sim \varepsilon} \begin{bmatrix}\displaystyle r + \gamma \max{a'} Q_{i}(s', a') | s, a \end{bmatrix} $$

Q-learning: Use a function approximator to estimate the action-value funciton ($\theta$ is funciton parameters i.e. weights)

$$ Q(s, a; \theta) \approx Q^*(s, a) $$

If the funciton approximator is a deep neural network, then it's called Deep Q-Learning

Q-Learning

Q Learning is a strategy that finds the optimal action selection policy for any Markov Decision Process

  • It revolves around the notion of updating Q values which denotes value of doing action a in state s. The value update rule is the core of the Q-learning algorithm.

Q learning algorithm

Training Strategies

Background

  • Learning from batches of consecutive samples is bad.
    • Samples are correlated => Inefficient learning
    • Can lead to bad feedback loops (bad Q-value leads to bad actions and maybe leads to bad states and so on)

Experience Replay

Policy Gradients

Definitions

  • Class of parametrized policies: $\prod = {\pi_\theta \theta \in \mathbb{R}^m }$
  • Value for each policy: $J(\theta) = \mathbb{E} \begin{bmatrix}\displaystyle \sum_{t\geq 0} \gamma^t r_t | \pi_\theta \end{bmatrix}$
  • Optimal policy: $\theta^* = \arg \max_\theta J(\theta)$

To find the optimal policy: Gradient ascent on policy parameters!

REINFORCE algorithm

When sampling a trajectory $\tau$, we can estimate $J(\theta)$ with the gradient estimator:

$$ \nabla_\theta J(\theta) \approx \sum_{t\geq 0} r(\tau) \nabla_\theta \log \pi_\theta(a_t|s_t) $$

Intuiiton

  • If reward of trajectory $r(\tau)$ is high, push up the probabilities of the actions seen
  • If reward of trajectory $r(\tau)$ is low, push down the probabilities of the actions seen

Variance Reduction (typically used in Vanilla REINFORCE)

  • First idea: Push up probabilities of an aciton seen, only by the cumulative future reward from that state
  • Second idea: Use discount factor $\gamma$ to ignore delayed effects

Baseline function

  • Third idea: Introduce a baseline function dependent on the state. (process the raw value of a trajectory)

Actor-Critic Algorithm

Combine Policy Gradients and Q-learning by training both an actor (the policy ($\theta$)) and a critic (the Q-function ($\phi$))

$$ A^\pi (s, a) = Q^\pi (s, a) - V^\pi (s) $$

Deep Q-network (DQN)

Deep version of Q-learning

DDPG(Deep Deterministic Policy Gradient)

Actor-Critic + DQN

Summary

Policy Gradients Q-Learning
very general but suffer from high variance so requires a lot of samples does not always work but when it works, usually more sample-efficient
Challenge: sample-efficiency Challenge: exploration
Grarantees: Converges to a local minima of $J(\theta)$, often good enough Guarantees: Zero guarantees since you are approximating Bellman equation with a complicated funciton approximator
Learning \ Sampling $\epsilon$ greedy random
$\epsilon$ Sarsa ? ?
(Max) greedy Q-learning ? (off-policy)
random ? ? (on-policy)

Resources

Book

Reinforcement Learning: An Introduction - pdf with outlines - (old online version)

  • Introduction
  • I. Tabular Solution Methods
    • Ch2 Multi-armed Bandits 多臂老虎機
      • Ch2.2 Action-value Methods
      • Ch2.7 Upper-Confidence-Bound Action Selection
      • Ch2.8 Gradient Bandit Algorithms
    • Ch3 Finite Markov Decision Processes
      • Ch3.2 Goals and Rewards
      • Ch3.3 Returns and Episodes
      • Ch3.5 Pilicies and Value Functions
      • Ch3.6 Optimal Policies and Optimal Value Functions

Others' Solution

Tutorial

Q Learing

MOOC

Article

Github

Good Example

Wikipedia