Skip to content

Latest commit

 

History

History
367 lines (273 loc) · 12.7 KB

정규화.md

File metadata and controls

367 lines (273 loc) · 12.7 KB

정규화(Normalization)

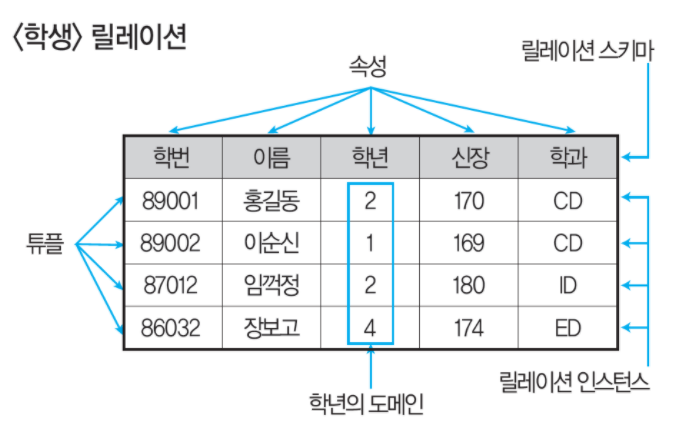
  • 정규화는 이상현상이 있는 릴레이션을 분해하여 이상현상을 없애는 과정
  • 릴레이션을 분해하여 여러개의 릴레이션을 생성하게 된다.
  • 이를 단계별로 구분하여 정규화 단계가 높아질수록 이상(Anomaly)현상은 줄어들게 된다.

릴레이션

  • 테이블을 릴레이션이라고 한다.
  • 속성 = 필드 = 열 = 컬럼
  • 튜플 = 레코드 = 행
  • 도메인: 필드에 입력 가능한 값
    (ex: 이름, 전화번호)
    릴레이션

정규화의 장단점

장점

  • 데이터베이스 변경 시 이상 현상(Anomaly)를 제거할 수 있다.
  • 새로운 데이터 형의 추가로 인한 확장 시, 그 구조를 변경하지 않아도 되거나 일부만 변경해도 된다.
  • 데이터베이스와 연동된 응용 프로그램에 최소한의 영향만을 미치게 되어 응용 프로그램의 생명을 연장시킨다.

단점

  • 릴레이션의 분해로 인해 릴레이션 간의 JOIN 연산이 많아진다.
  • Query에 대한 응답 시간이 느려질 수도 있다.

제 1 정규형 (1NF)

테이블의 컬럼이 원자값을 갖도록 분해한다.

조건

  1. 각 컬럼이 하나의 값(속성)만을 가져야 한다.
  2. 하나의 컬럼은 같은 종류나 타입의 값을 가져야 한다.
  3. 각 컬럼이 유일한(unique) 이름을 가져야 한다.
  4. 컬럼의 순서가 상관 없어야 한다.

-> 즉, 하나의 칸에 하나의 데이터만 보관하게 해야한다.

아래와 같은 테이블이 있다.

수강강좌

학번 이름 강좌이름
101 최다인 운영체제, 알고리즘
102 이규현 자료구조
103 김지원 알고리즘
104 최혁순 자료구조, 운영체제
  • 최다인, 최혁순의 경우 여러개의 강의를 듣고 있기 때문에 원자성을 만족하지 못한다.
  • 강좌를 수강신청한 사람들을 찾으려면 문자열 파싱을 통해 찾아야한다.
  • 프로그램명 수정도 쉽지 않다.
제 1 정규형을 활용하면

학번 이름 강좌이름
101 최다인 운영체제
101 최다인 알고리즘
102 이규현 자료구조
103 김지원 알고리즘
104 최혁순 자료구조
104 최혁순 운영체제

제 2 정규형 (2NF)

제 1정규형을 만족하고 부분적 종속(partial dependency)을 제거하여 모든 컬럼이 완전 함수 종속을 만족하게 한다.

조건

  1. 제 1정규형을 만족해야 한다.
  2. 모든 컬럼이 완전 함수 종속을 만족해야한다

-> 즉, 현재 테이블의 주제와 관련 없는 컬럼을 다른 테이블로 빼는 작업

부분적 종속과 완전 함수 종속

  • 부분적 종속: 기본키 중 특정 컬럼에만 종속되는 것
  • 완전 함수 종속: 기본키의 부분집합이 결정자가 되어선 안된다는 것
    즉, 테이블의 기본키가 복합키(두 개 이상의 컬럼으로 구성된 키)일 때, 기본키의 부분집합이 결정자가 되어서는 안된다

위의 테이블을 조금 더 확장해보자

수강정보

학번 강좌이름 성적 지도교수
101 운영체제 4.0 김운영
101 알고리즘 3.5 박코테
102 자료구조 4.5 왕자료
103 알고리즘 2.5 박코테
104 자료구조 4.5 왕자료
104 운영체제 4.0 김운영

이 테이블의 기본키는 {학번, 강좌이름}의 복합키이고, '성적'을 결정한다. 그런데 여기서 {강좌이름}은 '지도교수' 컬럼을 결정할 수 있다.

이런 경우가 완전 함수 종속인 경우이다. 박코테 교수의 강좌가 컴퓨터 구조로 바뀔경우 모든 row를 탐색해 바꿔주어야한다.

제 2 정규형을 활용하면

수강

학번 강좌이름 성적
101 운영체제 4.0
101 알고리즘 3.5
102 자료구조 4.5
103 알고리즘 2.5
104 자료구조 4.5
104 운영체제 4.0

지도

강좌이름 지도교수
운영체제 김운영
알고리즘 박코테
자료구조 왕자료
  • 기존의 테이블에서 지도교수를 분해하여 별도의 테이블을 만들어 제 2정규형을 만족시켰다.
  • 지도 테이블에서 알고리즘 Row에 해당하는 강좌 이름 하나만 수정해도 싹 다 변경된다.

제 3 정규형 (3NF)

기본키를 제외한 속성들 간에 이행 종속성이 없도록 테이블을 분해한다.

조건

  1. 제 2정규형을 만족해야한다
  2. 기본키를 제외한 속성들 간의 이행 종속성이 없어야한다

이행 종속성

  • A->B, B->C 일 때, A->C가 성립하면 이행 종속이다.

ex) 장학금

학번 수상 상금
101 대상 100만원
102 최우수상 70만원
103 우수상 50만원
104 우수상 50만원

학번(A) -> 수상(B), 수상(B) -> 상금(C)이다. 결국 학번(A) -> 상금(C) 이므로 이행 종속성이 존재하여 제 3정규형을 만족하지 않는다.

  • 우수상의 상금이 30만원으로 변경될경우 모든 우수상 Row를 찾아 바꿔야한다.
제 3 정규형을 활용하면

등수

학번 수상
101 대상
102 최우수상
103 우수상
104 우수상

장학률

수상 상금
대상 100만원
최우수상 70만원
우수상 50만원

위와 같이 분해하여 제 3정규형을 만족시킬 수 있다.

BCNF (Boyce-Codd Normal Form) : 제 3 정규형의 강화된 버전

모든 결정자가 후보키가 되도록 테이블을 분해한다.

조건

  1. 제 3정규형을 만족해야한다.
  2. 모든 결정자가 후보키 집합에 속해야 한다.

ex)특강수강

학번 특강이름 지도교수
101 기술 면접이란 씨에스
102 기술 면접이란 씨에스
102 취업 성공 전략 이취업
103 코테 박살내기 최알고
101 코테 박살내기 박리즘

이 테이블에서 기본키는 **{학번, 특강이름}**으로 '지도교수'를 결정하고 있다. 또한 '지도교수'는 '특강이름'을 결정할 수 있다. 같은 과목을 다른 강사가 가르칠 수도 있어서 프로그램 -> 강사 종속은 성립하지 않는다. (제 2정규형 만족) 여기서 **'지도교수'**는 '특강이름'을 결정하는 결정자 이지만 후보키는 아니다. 이런 경우 지도교수 '씨에스'의 특강이름이 '면접 성공의 이해'로 변경되었다면 두개의 row를 갱신해야하는 문제가 생긴다.

BCNF를 활용하면

특강신청

학번 지도교수
101 씨에스
102 씨에스
102 이취업
103 최알고
101 박리즘

특강지도

특강이름 지도교수
기술 면접이란 씨에스
취업 성공 전략 이취업
코테 박살내기 최알고
코테 박살내기 박리즘
  • 지도교수가 기본키로 세팅된 테이블로 분해됐다.

위와 같이 분해하여 제 3정규형을 만족시킬 수 있다.

제 4 정규형 (4NF)

다치 종속이 존재하지 않도록 분해한다

조건

  1. BCNF를 만족해야 한다.
  2. 최소 3개의 컬럼이 존재한다.
  3. R(A,B,C)가 있을 때, A와 B 사이에 다치 종속성이 있을 때 B와 C가 독립적이다.

다치 종속

  • A->B 일 때, 하나의 A값에 여러 개의 B값이 존재하면 다치 종속성을 가진다고 한다.

ex)학생정보

학번 과목 동아리
101 알고리즘 노래
102 자료구조 요리
103 자료구조 춤
103 자료구조 노래
103 운영체제 춤
103 운영체제 노래

103번 학생은 '자료구조', '운영체제'를 수강하고 / '춤', '노래' 동아리에 가입되어 있다. 여기서 '과목'과 '동아리'는 관계가 없는 독립적 관계지만 중복이 발생하고 있다. 과목과 동아리는 관계없는 독립적인 관계지만, 중복이 발생하게 된다. '회원번호' 컬럼에 '과목'과 '동아리'가 다치 종속 되어있는 상태이다.

제 4 정규형을 활용하면

수강정보

학번 과목
101 알고리즘
102 자료구조
103 자료구조
103 운영체제

동아리정보

학번 동아리
101 노래
102 요리
103 춤
103 노래

여전히 다치 종속성을 가지지만, 2개 이상의 컬럼이 1개의 컬럼에 다치 종속되지는 않아 제 4정규형을 만족한다.

제 5 정규형 (5NF)

중복을 제거하기 위해 분해할 수 있을 만큼 전부 분해한다.

  • 제 4 정규형을 만족하는 상태
  • 조인 종속이 없어야한다.
  • 조인 연산을 했을 때 손실이 없어야한다. (원상복구 할 수 있도록 분리한 상태)

조인 종속

  • 다치 종속의 좀 더 일반화된 형태
  • 만약 하나의 릴레이션을 여러 개의 릴레이션으로 무손실 분해했다가 다시 결합할 수 있다면 조인 종속이라고 한다.
  • 쉽게 말해.. 분해한걸 다시 원상복구 시킬 수 있느냐?

image

너무 이상적.. 오히려 조인 종속이 존재하는 릴레이션이 사용하기 편하다.

ex)학생정보

이름 과목 동아리
김기술 알고리즘 노래
김기술 알고리즘 요리
김기술 자료구조 노래
김기술 자료구조 요리
김기술 운영체제 노래
김기술 운영체제 요리

이름과 과목은 연관성이 있고, 이름과 동이라 역시 연관성이 존재한다. 즉, 이름 속성을 기준으로 연관성을 가지므로 조인 종속성이 존재한다. 따라서 이름, 과목/과목,동아리/이름,동아리 3가지 테이블로 분해해야한다.

제 5 정규형을 활용하면

이름, 과목

이름 과목
김기술 알고리즘
김기술 자료구조
김기술 운영체제

과목, 동아리

과목 동아리
알고리즘 노래
알고리즘 요리
자료구조 노래
자료구조 요리
운영체제 노래
운영체제 요리

이름, 동아리

이름 동아리
김기술 노래
김기술 요리

2개의 테이블의 조인으로는 본래의 릴레이션 형성이 불가능하다. 3개의 테이블을 전부 사용하여 조인해야 본래 릴레이션으로 복구가 가능하다.

정리

  • 제 1정규화: 모든 컬럼이 원자값을 가진다.
  • 제 2정규화: 기본키의 부분 집합이 결정자가 되면 안된다.
  • 제 3정규화: 이행 종속(A->B, B->C일 때 A->C)이 있으면 안된다.
  • BCNF: 후보키가 아닌 결정자가 있으면 안된다.
  • 제 4정규화: A->B일 때 하나의 A값에 여러 개의 B값이 존재하면 안된다(다치 종속X).
  • 제 5정규화: 조인 종속성이 없어야한다.

Reference