Let’s start with the basic model we will use in this chapter. The model consists of an environment and an agent who lives in this environment.
##Environment Given below is a landscape of N×M cells. The edges are connected to derive a torus – donut shaped – environment (Figure 2).
When we put agents on the landscape they will not experience any edges. Each cell can contain a resource unit. This resource unit provides an amount of energy R to an agent, if the agent collects it. If an agent has collected the resource unit of a cell, a new resource unit can appear on the cell with a probability pr.
To implement this in NetLogo we will look at each patch to determine whether there are resources on the cell. If there are no resources on the cell then there is a chance prob that new resources will be added to the cell. In a simple model the only options available are resources on the cell or no resources on the cell. This can be implemented as below. The figure to the right shows a screen shot of such a landscape.

Figure 3: Screenshot of the landscape.
if pcolor = black [
if random-float 1 < prob
[
set pcolor green
]
]
##Agents Agents need energy to survive. Each time step they use m units of energy. This is their metabolism. They can derive energy from collecting resource units from the landscape. Agents move randomly around and if they are on a cell with a resource unit, they collect this resource unit. If agents have run out of energy they will die. On the other hand, if their energy level reaches more than bt, the birth threshold, the agent will split into two agents. This cloning is a simplistic way of simulating reproduction.
We will now discuss a NetLogo program that simulates the model described above.
First, we have to define that agents will have the attribute energy. This is the only turtle attribute that we need to include. Of course the turtles already contain a number of default attributes such as location, color and heading.
turtles-own [energy]
To initialize the model we have to define the initial level of energy the agents have. In this example, we assume that at the start all agents have 10 units of energy. We put the agents randomly on the landscape and represent them as white dots.
We also need to initialize the environment. For each patch we flip a coin to define whether the patch has a resource unit or not. If the patch has a resource unit we define the color of the patch green, otherwise it remains black. Note that we used a standard attribute of the patch to define whether a resource unit is available, and so we will not have to define a new attribute for patches. The initial density of resource is assumed to be equal to initial-density, which is a value defined by a slider in the interface.
to setup
ca
set-default-shape turtles "dot"
create-turtles number [
set energy 10
set color white
setxy random-xcor random-ycor
]
ask patches [
if random-float 1 < initial-density [set pcolor green]]
end
Once we click on go the agents will make a number of decisions within each tick. The first problem we face is which order decisions need to be made. Will an agent eat first and then move? Does each agent perform the same actions in the same order? In which order do we update the agents? Will some agents get priority? These decisions on the order in which decisions are made can have important consequences on the outcomes of the model. In our simple model it will not have a huge impact. We assume that the order of the actions is movement, eating, metabolism, reproduction, and dying.
First all agents will move before we move to the next action. You see that the agents change their direction randomly before taking one step forward. To model the random type of movement we change the direction of the agents each time step. The heading of the agent is changed by moving it to the right. The number of degrees it moves to the right is a random number between 0 and 45. Then the agent moves to the right again, also at a randomly drawn number between 0 and 45. On average the heading of the agent is directed straight forward, but most agents will change its heading a small amount to the right or left. With a small change the agent will change it’s heading by several degrees in one step. After the direction is defined, the agent will make one step forward using fd 1.
ask turtles [
rt random 45
lt random 45
fd 1]
If they are on a patch that is colored green (thus has a resource) the agent will collect the resource unit, which will generate penergy (slider value) units of energy. It is possible that more than one agent is on a cell. In that case the agent who has drawn first to eat will collect the resource unit and will put the color of the cell equal to black.
ask turtles [
if (pcolor = green) [
set pcolor black
set energy energy + penergy]]
```
Then the energy level of all agents is reduced with the amount `metabolism` (slider value).
ask turtles [set energy energy - metabolism]
If the energy level is more than `birth-threshold` (slider value), we first half the energy level of the agent before we generate a copy. `hatch` means that the agent is cloned. If we don’t half the energy first, we will get two agents with more energy than `birth-threshold.` In such a situation, the system would generate energy by producing offspring, which is not possible.
<br>*
Figure 4: Screenshot of a typical run of the model.8.*
ask turtles [ if energy > birth-threshold [ set energy (energy / 2) hatch 1]] ``` Finally, if an agent has a negative unit of energy, the agent will die and is removed from the system.
ask turtles [if energy < 0 [die]]
We also need to update the resource units on the patches every time step. If a patch has no resource unit, we assume that with a probability replenishment-rate (slider-value) a new resource unit will be added to the patch. The NetLogo model for this was discussed above when we discussed the environment.
Now we can simulate the model in NetLogo. In Figures 4 and 5 you see some typical results of the model. You will see that the population level depends critically on the level of the parameters, which can be changed by the sliders. If metabolism is high compared to energy per resource unit, the population is more quick to die out. In other situations we see that the population reaches a somewhat stable level of resources, or has some periodic fluctuations. Why do we get fluctuations of the population size? The agents eat up the resources quickly and produce a lot of offspring. The increasing population causes a scarcity of resource units. Due to the scarcity, agents cannot get enough energy to maintain their metabolism and more agents will die than are born. When the population size drops, more resources become available for those who survived, etc.
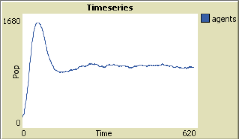
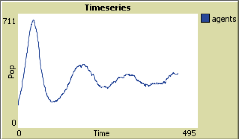
*
Figure 5: Two possible outcomes of the population level over time.*
How many agents can survive in this landscape? The default parameters of the agents are
metabolism = 1
birthrate = 20
foodenergy = 3
The environment is 100 x 100 cells, thus 10,000 cells. Suppose the environment produces feedenergy * replenishment-rate * 10,000 cells, then the environment produces 300 units of energy. This could feed 300 agents. However, agents will have to move to another cell to find food. Agents move randomly so it will not be the most efficient exploration. At least we can expect that the total number of agents that survive over the longer term will be lower than 300 agents. When we run the model we see that the population stabilizes around 200 agents. For each increase in the replenishment rate we can expect a linear increase of the population.
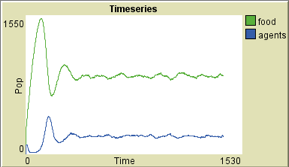
*
Figure 6: Resource size and population size using a replenishment rate equal to 0.01.*
NETLOGO EXAMPLE: POPULATION DYNAMICS
Model: Right click on the Link and Save it. Open Netlogo and Run it with NetLogo.