LeetCode 116. Populating Next Right Pointers in Each Node

[Woodyiiiiiii]

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

• You may only use constant extra space.
• Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
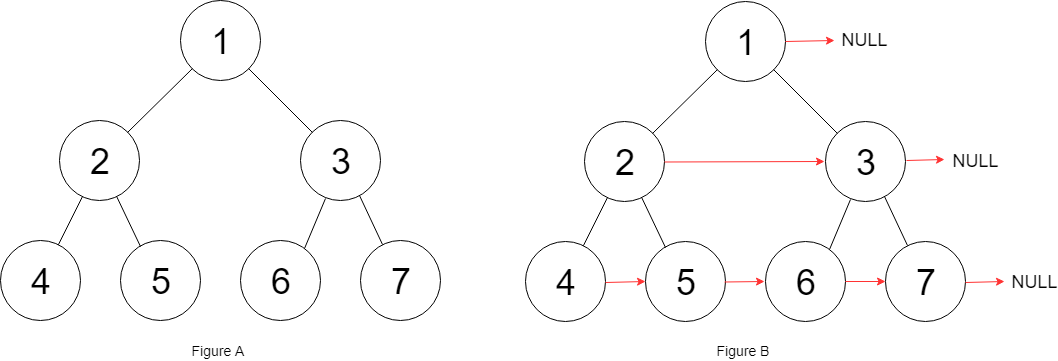
Explanation: Given the above perfect binary tree (Figure A), 
your function should populate each next pointer to point to i
ts next right node, just like in Figure B. The serialized output 
is in level order as connected by the next pointers, 
with '#' signifying the end of each level.

---

我首先想到的思路就是BFS层次遍历，将前节点指向同层次的下一个节点：

// BFS层次遍历
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        Deque<Node> queue = new LinkedList<>();
        queue.offerLast(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; ++i) {
                Node node = queue.pollFirst();
                if (i != size - 1) {
                    node.next = queue.peek();
                }
                if (node.left != null) {
                    queue.offerLast(node.left);
                }
                if (node.right != null) {
                    queue.offerLast(node.right);
                }
            }
        }
        return root;
    }
}

当然这种方法利用额外空间，并且没有利用题目条件中的“完全二叉树”的特性。题目Follow up中也提到了可以用DFS，只要保证栈空间在这种题目环境下不占额外空间。

从“完全二叉树”的特性出发，使用DFS深度遍历(先序遍历)，如果是当前节点的左节点，指向当前节点的右节点(右节点一定存在)；如果是当前节点的右节点，则指向当前节点的下一个节点的左节点(如果不为空)，因为深度遍历的关系已经保证前一个节点有next节点。

// DFS 层次遍历 2
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        dfs(root);
        return root;
    }
    public void dfs(Node node) {
        if ((node == null)
            || (node.left == null && node.right == null)) {
            return;
        }
        if (node.left != null) {
            node.left.next = node.right;
        }
        if (node.right != null) {
            node.right.next = node.next != null ? node.next.left : null;
        }
        dfs(node.left);
        dfs(node.right);
    }
}

还有一种做法，也是一般题目下的DFS层次遍历，以层数作为标志，定义一种层数节点数据结构，属性是层数和所属层数最新节点，然后先序遍历：

// DFS 层次遍历
class LevelNode {
    public int level;
    public Node pre;
    public LevelNode(int level, Node pre) {
        this.level = level;
        this.pre = pre;
    }
}
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        List<LevelNode> levelNodes = new LinkedList<>();
        dfs(root, levelNodes, 1);
        return root;
    }
    public void dfs(Node node, List<LevelNode> levelNodes, int l) {
        if (node == null) {
            return;
        }
        if (l > levelNodes.size()) {
            levelNodes.add(new LevelNode(l, node));
        }else {
            LevelNode ln = levelNodes.get(l - 1);
            ln.pre.next = node;
            ln.pre = node;
        }
        dfs(node.left, levelNodes, l + 1);
        dfs(node.right, levelNodes, l + 1);
    }
}

正常的DFS层次遍历：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new LinkedList<>();
        if (root == null) {
            return res;
        }
        dfs(root, res, 1);
        return res;
    }
    public void dfs(TreeNode node, List<List<Integer>> res, int l) {
        if (node == null) {
            return;
        }
        if (l > res.size()) {
            List<Integer> list = new LinkedList<Integer>();
            list.add(node.val);
            res.add(list);
        }else {
            List<Integer> list = res.get(l - 1);
            list.add(node.val);
        }
        dfs(node.left, res, l + 1);
        dfs(node.right, res, l + 1);
    }
}

这题还有一种巧妙的解法，利用两个节点，start表示每层的最左节点，cur节点用来遍历当前层次所有节点，每次保证下一个层次的节点的next指针指向。

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return null;
        }
        Node start = root, cur = null;
        while (start.left != null) {
            cur = start;
            while (cur != null) {
                cur.left.next = cur.right;
                if (cur.next != null) {
                    cur.right.next = cur.next.left;
                }
                cur = cur.next;
            }
            start = start.left;
        }
        return root;
    }
}

---

参考资料：

• https://leetcode.com/problems/populating-next-right-pointers-in-each-node/
• https://www.cnblogs.com/grandyang/p/4051321.html
• https://leetcode.com/problems/binary-tree-level-order-traversal/