- Reverse a given queue with and without using recursion
- Give an algorithm for reversing a queue Q. Only following standard operations are allowed on queue.
- enqueue(x) : Add an item x to rear of queue.
- dequeue() : Remove an item from front of queue.
- empty() : Checks if a queue is empty or not.
- Using the Last In First Out (LIFO) property of stack to get the last element of queue as the topmost element of stack.
- Add the stack elements again to the queue till stack is empty, which would give the queue in reverse order.
begin reverseQueueWithoutRecursion(queue)
stack s
while(queue is not empty)
s.push(queue.front());
q.pop()
end of while
while( stack is not empty)
q.push(s.top())
s.pop()
end of while
end reverseQueueWithoutRecursion
- O(n)
- O(n)
- Given a queue, write a recursive function to reverse it.
- Standard operations allowed :
- enqueue(x) : Add an item x to rear of queue.
- dequeue() : Remove an item from front of queue.
- empty() : Checks if a queue is empty or not.
-
Store the front element of the queue in a variable and pop that element from queue.
-
Continue Step 1 until queue is empty.
-
Push the popped element in the resultant queue.
begin reverseQueueWithRecursion(queue)
if(queue is empty)
return
end of if
data = queue.front()
queue.pop()
reverseQueueWithRecursion(queue)
queue.push(data)
end reverseQueueWithRecursion
- O(n)
- O(n) (As recursion uses stack concept)
- Implementation of Queue using Array and performing different operations such as insertion, deletion and display of elements in a queue.
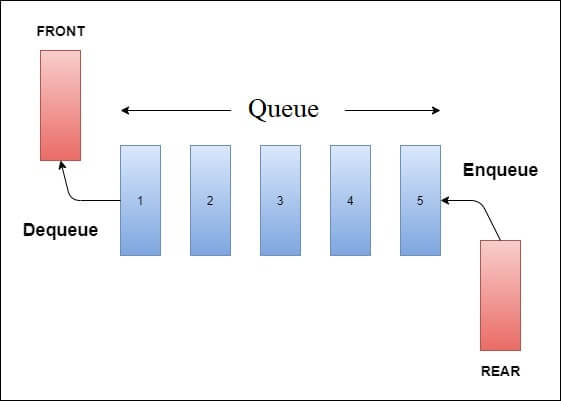
- Queue is a linear data structure which has two ends, one for insertion of elements and other for deletion of elements.
- The first end is called ‘Rear’ and the later is called ‘Front’.
- Elements are inserted from Rear end and deleted from Front end.
- Queues are called First In First Out (FIFO) list, since the first element in a queue will be the first element out of the queue.
There are 3 main operations.
- Enqueue: Adds an item to the queue. If the queue is full, then it is said to be an Overflow condition.
- Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition.
- Display: All the elements of the queue are displayed, starting from the front index to the rear.
- For insertion
STEP 1: IF REAR == N-1
Return OVERFLOW
Goto STEP 3
STEP 2: IF REAR != N-1
Set ARR[REAR] = INTEGER
INCREMENT REAR BY 1
{END OF LOOP}
STEP 3: EXIT LOOP
- For deletion
STEP 1: IF (FRONT==0 AND REAR==-1) OR FRONT==REAR+1
Return UNDERFLOW
Goto STEP 2
ELSE
Return ARR[FRONT]
INCREMENT FRONT BY 1
STEP 2: EXIT
- For display
for i from front to rear
print array[i]
- Enqueue: O(1) time
- Dequeue: O(1) time
- Display: O(N) time
- O(1)
- Memory wastage : The space of the array, which is used to store queue elements, can never be reused to store the elements of that queue because the elements can only be inserted at front end and the value of front might be so high so that, all the space before that, can never be filled.
- Implementation of Queue using Linked List and performing different operations such as insertion, deletion and display of elements in a queue.
- Queue is a linear data structure which has two ends, one for insertion of elements and other for deletion of elements.
- In linked list implementation of a queue, the last inserted node is always pointed by 'rear' and the first node is always pointed by 'front'.
- The queue which is implemented using a linked list can work for an unlimited number of values.
- Queue using linked list can work for the variable size of data (No need to fix the size at the beginning of the implementation).
There are 3 main operations.
- Enqueue: Adds an item to the queue. If the queue is full, then it is said to be an Overflow condition.
- Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition.
- Display: All the elements of the queue are displayed, starting from the front index to the rear.
- For insertion
Step 1: Allocate the space for the new node NEWNODE
Step 2: SET NEWNODE -> DATA = VAL
Step 3: IF FRONT = NULL
SET FRONT = REAR = PTR
SET FRONT -> NEXT = REAR -> NEXT = NULL
ELSE
SET REAR -> NEXT = NEWNODE
SET REAR = NEWNODE
SET REAR -> NEXT = NULL
[END OF IF]
Step 4: END
- For deletion
Step 1: Take TEMP=FRONT
Step 2: IF FRONT = NULL
Write " Underflow "
Go to Step 5
[END OF IF]
Step 3: SET TEMP = FRONT
Step 4: SET FRONT = FRONT -> NEXT
Step 5: FREE TEMP
Step 6: END
- For display
Step 1: Set TEMP = FRONT [Initializes pointer TEMP]
Step 2: Repeat Steps 3 and 4 while TEMP != NULL
Step 3: Apply PROCESS to TEMP -> DATA
Step 4: Set TEMP = TEMP -> NEXT
[End of Step 2 loop]
5. Exit
- Enqueue: O(1) time
- Dequeue: O(1) time
- Display: O(N) time
- O(1)
- The benefit of implementing queue using linked list over arrays is that it allows to grow the queue as per the requirements,i.e, memory can be allocated dynamically.
- Implementation of Circular Queue using Array and performing different operations such as insertion, deletion and display of elements in a circular queue.
- Circular Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle.
- It is also called ‘Ring Buffer’.
- In a normal Queue, we can insert elements until queue becomes full. But once queue becomes full, we can not insert the next element even if there is a space in front of queue.
- This problem is solved using Circular Queue.
There are 3 main operations.
-
Enqueue: Adds an item to the queue. If the queue is full, then it is said to be an Overflow condition.
-
Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition.
-
Display: All the elements of the queue are displayed, starting from the front index to the rear.
- For insertion
Step 1: Check if the queue is full (Rear + 1 % Maxsize = Front)
Step 2: If the queue is full, there will be an Overflow error
Step 3: Check if the queue is empty, and set both Front and Rear to 0
Step 4: If Rear = Maxsize - 1 & Front != 0 (rear pointer is at the end of the queue and front is not at 0th index), then set Rear = 0
Step 5: Otherwise, set Rear = (Rear + 1) % Maxsize
Step 6: Insert the element into the queue (Queue[Rear] = x)
Step 7: Exit
- For deletion
Step 1: Check if the queue is empty (Front = -1 & Rear = -1)
Step 2: If the queue is empty, Underflow error
Step 3: Set Element = Queue[Front]
Step 4: If there is only one element in a queue, set both Front and Rear to -1 (IF Front = Rear, set Front = Rear = -1)
Step 5: And if Front = Maxsize -1 set Front = 0
Step 6: Otherwise, set Front = Front + 1
Step 7: Exit
- For display
Step 1 - Check whether queue is EMPTY. (front == -1)
Step 2 - If it is EMPTY, then display "Queue is EMPTY!!!" and terminate the function.
Step 3 - If it is NOT EMPTY, then define an integer variable 'i' and set 'i = front'.
Step 4 - Check whether 'front <= rear', if it is TRUE, then display 'queue[i]' value and increment 'i' value by one (i++). Repeat the same until 'i <= rear' becomes FALSE.
Step 5 - If 'front <= rear' is FALSE, then display 'queue[i]' value and increment 'i' value by one (i++). Repeat the same until'i <= SIZE - 1' becomes FALSE.
Step 6 - Set i to 0.
Step 7 - Again display 'cQueue[i]' value and increment i value by one (i++). Repeat the same until 'i <= rear' becomes FALSE.
- Enqueue: O(1) time
- Dequeue: O(1) time
- O(1)
- The key advantage of a circular queue over a normal queue is effective utilization of storage space or memory.
- CPU scheduling
- Memory management
- Traffic Management
- Implementation of Circular Queue using Linked List and performing different operations such as insertion, deletion and display of elements in a circular queue.
-
Circular Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle.
-
When we implement circular Queue using linked list it is similar to circular linked list except there is two pointer front and rear in circular Queue where as circular linked list has only one pointer head.
There are 3 main operations.
- Enqueue: Adds an item to the queue. If the queue is full, then it is said to be an Overflow condition.
- Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition.
- Display: All the elements of the queue are displayed, starting from the front index to the rear.
- For insertion
Step 1: if (((FRONT == 0) and (REAR == N - 1)) or (REAR == FRONT - 1)) // Condition for overflow
Step 2: Print “Queue Overflow”
Step 3: end
Step 4: else if (FRONT == -1) // Inserting in an Empty Queue
Step 5: FRONT = REAR = 0
Step 6: end ifelse if (REAR == N - 1) // Inserting after the last element
Step 7: REAR = 0
Step 8: end ifelse
Step 9: REAR = REAR + 1 // Increment REAR
Step 10: end else
Step 11: QUEUE [REAR]= element
Step 12: end
- For deletion
Step 1: if(FRONT == -1) // Condition for underflow
Step 2: Print “Queue Underflow”
Step 3: end Dequeue
Step 4: end if
Step 5: Temp = QUEUE[FRONT] // Copy FRONT in a temporary variableif(FRONT == REAR) // The queue contains only one node
Step 6: FRONT = REAR = -1
Step 7: end ifelse if (FRONT == N - 1) // If FRONT is the last node
Step 8: front = 0 // Make FRONT as the first node
Step 9: end ifelse
Step 10: FRONT = FRONT + 1 // Increment FRONT
Step 11: end else
Step 12: end Dequeue
- For display
Step 1: Set TEMP = FRONT [Initializes pointer TEMP]
Step 2: Repeat Steps 3 and 4 while TEMP->NEXT != FRONT
Step 3: Apply PROCESS to TEMP -> DATA
Step 4: Set TEMP = TEMP -> NEXT
[End of Step 2 loop]
Step 5: Apply PROCESS to TEMP -> DATA
Step 6: Exit
- Enqueue: O(1) time
- Dequeue: O(1) time
- O(1)
- The key advantage of a circular queue over a normal queue is effective utilization of storage space or memory.
- Linked list provide the facility of dynamic memory allocation so it is easy to create.
- We are given a stack data structure with push and pop operations, the task is to implement a queue using instances of stack data structure and operations on them.
- Queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle
- When we implement circular Queue using linked list it is similar to circular linked list except there is two pointer front and rear in circular Queue where as circular linked list has only one pointer head.
There are 3 main operations.
- Enqueue: Adds an item to the queue.
- Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition and an error message is displayed.
- Empty: Tells whether a queue is empty or not.
- For enqueue
Step 1: push element into stack1
- For dequeue
Step 1: if(s1.empty() && s2.empty()) // Condition for underflow
Step 2: Print “error”
Step 3: end Dequeue
Step 4: end if
Step 5: if (s2.empty)
Step 6: while(!s1.empty())
Step 7: s2.push(s1.pop())
Step 8: s1.pop()
Step 9: end if
Step 10: topval = s2.top()
Step 11: s2.pop()
Step 12: return topval
Step 13: end dequeue
- For empty
Step 1: if(s1.empty() && s2.empty())
Step 2: return true
Step 3: else
Step 4: return false
Step 5: Exit
- Enqueue: O(1) time
- Dequeue: O(n) time
- O(n)
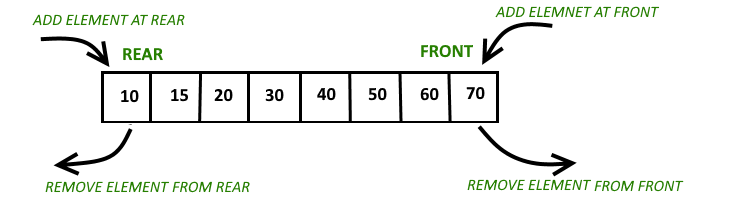
- Deque or Double Ended Queue is a generalized version of Queue data structure that allows insert and delete at both ends. We are ussing array to implement it
-
Some basic operations of dequeue are −
-
insert_at_beg(): inserts an item at the front of Dequeue.
-
insert_at_end(): inserts an item at the rear of Dequeue.
-
delete_fr_beg(): Deletes an item from front of Dequeue.
-
delete_fr_rear(): Deletes an item from rear of Dequeue.
-
- For insert_at_beg(int) :
If queue is not completely filled up, insert element at the front and update front and rear
Otherwise print overflow.
- For insert_at_end(int)
If queue is not completely filled up, insert element at the rear and update front and rear
Otherwise print overflow.
- For delete_fr_beg()
If queue is empty, print underflow otherwise delete the front element and update front.
- For delete_fr_end()
If queue is empty, print underflow otherwise delete the rear element and update rear.
- insert_at_beg(int): O(1) time
- insert_at_beg(int): O(1) time
- delete_fr_beg(): O(1) time
- delete_fr_end(): O(1) time
- O(n)