-
Notifications
You must be signed in to change notification settings - Fork 7
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
面试中需要知道的哈弗曼编码知识[data structure] #16
Comments
|
赞
|
|
先赞后看 |
|
非常清楚,再赞一下。所以核心算法就是这一段 while(trieNode.size() > 1){
Node left = getMin(trieNode);
Node right = getMin(trieNode);
Node parent = new Node('\0', (left.freq + right.freq), left, right);
trieNode.add(parent);
}提取list里最小的两个node,以他们为child组建一个parent node,放回到list里,直到list为空。 |
先前在亚马逊面试的第一道就碰到了哈弗曼树。虽然早有准备,不过匆忙之中写出的代码还是忽略了诸多要点。以下是鄙人对哈弗曼树的一些肤浅理解。诸君若要深入了解请务必亲自实践。
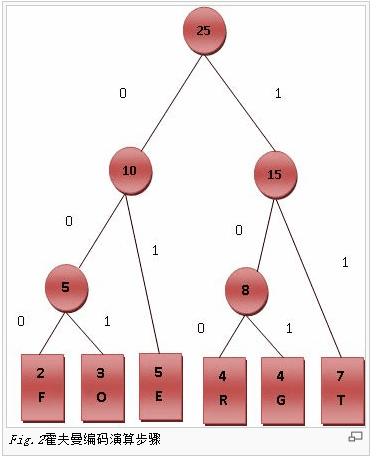
哈弗曼树主要应用于数据压缩、字符编码中。与大部分树的构建方式不同,哈弗曼树是自底而上构建的。算法的输入通常为字符串,根据字符出现的频率由小到大构建产生,其叶节点(且只有叶节点)为字符串的每一个字符。
其大致的原理是:
以下为部分代码:
树节点结构:
node类利用了java的Comparable接口,更为便捷地比较频率大小。
以下为关键的建树部分。面试时把这个写清楚就安全上垒了。其他的边角料顺着思路走下去即可。
trieNode是一个以ArrayList实现的container(此处可以使用最小优先队列), 作用是存储构建中的树节点。改方法传入的是freq,其定义是:
···Java
char[] input = s.toCharArray();
//tabulate freq
int[] freq = new int[256];
for(int i = 0; i < input.length; i++){
freq[input[i]]++;
}
···
input的char数组正是由算法输入的字符串s转化而来。依据假设其为ASCII(你需要向面试官指出),新建长度为256的整型数组,数组的index逐个对应ASCII的每个字符,通过for循环计算出每个字符的出现频率。
回到trieNode, buildTrie的第一个for循环将每个频率大于零的字符转为Node,加入ArrayList。for语句结束后的结果是trieNode里包含了所有频率大于零的字符的Node。while语句则是建树的过程。getMin()获取并删除trieNode中的频率最小Node,其代码就不再赘述。左节点的值应当比右节点小。parent则是父节点,用\0代替字符值,也符合非叶节点不含字符信息的定义。千万别忘了将新的父节点加入trieNode(我当时就忘了,不是不知道,是真的粗心啊)。while跳出时trieNode应该只剩根节点了,最后返回根节点,哈弗曼树的建树(压缩)部分就完成了。
以上完全可以用最小优先队列来代替ArrayList。getMin()也正是将顶部节点取出。大家可以自己练习。
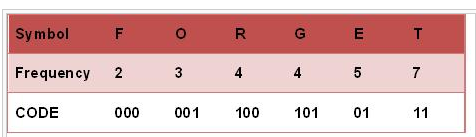
完成后的树,解码是非常容易的。每当从父节点先左移动时,就计入0,,反之向右则计入1。例如上图,f的编码是000,因为从root到f叶节点都是向左边移动(左-左-左),而O为001(左左右)。解码是注意到达叶节点时将指针复原至root即可。为此Node类也特意定义了isLeaf()方法。
匆忙之中就略过测试了。以下为代码来源:
http://algs4.cs.princeton.edu/55compression/Huffman.java.html
/_如有错误,请(不要太)严正地指出_/
The text was updated successfully, but these errors were encountered: